算法课程笔记-最小割问题

发表于 分类于 ， Valine：

前面介绍了两种使用随机算法（快速排序 和 随机选择算法），特点是每次执行的 时间复杂度不确定，但能够确定的得到正确的解。本篇中同样介绍一种随机算法 - Karger 算法， 用于求解 “最小割问题”。与前面几种随机算法不同的是，Karger 算法的时间复杂度是确定的，但得到的解不一定是正确的，然而，我们可以通过 多次 调用的方法，来提升得到正确解的概率。

1. 最小割问题

对于最小割问题，我们首先定义 “割（cut）”：割是指在 图 $G=(V, E)$ 中，分割出一个子节点集合 $S$, 满足$S \subset V, S \neq \emptyset, S \neq V$。一个 割的大小是指，完成上述区间分割，需要切断的 边的数量。所谓最小割问题，也就是在所有的 图的划分方案中，切割最少边的 划分方式。

如下面的图中，绿色线对应的 cut 大小为 2， 而红色线对应的 cut 大小为 3，分析整个图，我们可以发现，该图中 cut 最小值为 2，因此绿色线对应了该图中的一个 最小割。需要注意的是，最小割的方案不是唯一的，例如下图中，割出左下角一个结点也是一种 最小割 的方案。

由Kilom691，CC BY-SA 3.0，https://commons.wikimedia.org/w/index.php?curid=25997273

2. Karger 算法描述

对于最小割问题，如果使用暴力枚举的方案，总的时间复杂度为指数级别：$O(2^n)$ (因为 $C_n^1 + C_n^2 + …. C_n^{n-1} = 2^n - 2$)。为降低算法的时间复杂度， Karger 算法是一种可行的方案。具体的，Karger 算法的流程如下：

Step1: 在图中随机选择 一条边 $E_{u,v}$ 将其删除, 并将它两端的 结点 $u, v$ 收缩为一个 大的结点 $w$，$u$ 和 $v$ 与 $V/\{u,v\}$ 中结点相连的边全部修改为与 $w$ 相连。

step2: 重复执行 step1 中的步骤，直到图中仅剩余两个超级结点，这两个超级结点 确定一个割，两节点之间的 边的数量确定这个割的大小。

一个例子如下：

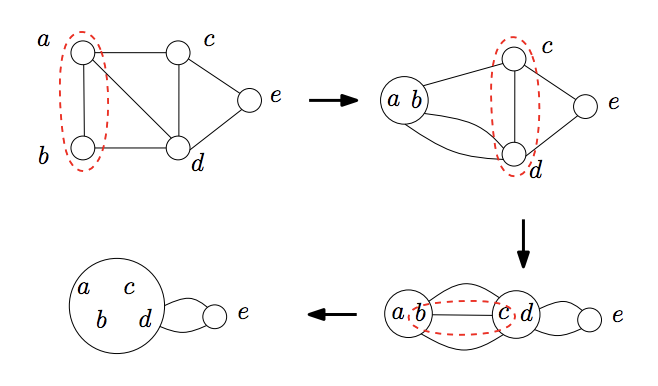
https://medium.com/@dev.elect.iitd/kargers-algorithm-d8067eb1b790

3. Karger 算法分析

Karger 算法收缩时，选择的边是随机的，那么执行一次该算法，恰好得到 最小割 的概率是多少呢？分析这个复杂问题之前，我们首先考虑，首次 收缩时，我们选择的边 为 min-cut 经过的边的概率。这里，我们假设 min-cut 的大小为 k，图中结点的数量为 n。由于 min-cut 为k，因此每个结点至少有 k 个边与之相连（反证，如果不这样，这个结点单独可以作为一个 cut，大小小于 k），因此总的边的数量为 $\frac{n\cdot k}{2}$，在这 $\frac{n \cdot k}{2}$ 条边中恰好选择到 最小割的 k 条边的概率为 $\frac{2}{n}$。

经过多次删除后，最终留下 min-cut 对应的 k 条边的 概率，可以通过条件概率的方式进行求解。这里，我们以最简单的情况举例，即 $P[\neg S_1 \land \neg S_2] = P[\neg S_2 | \neg S_1] \cdot P[\neg S_1]$, 这里的 $S_i$ 表示 第i次收缩，所选择的边，$\neg S_i$ 则表示 第 i 次收缩，没有选择 min-cut 对应的 k 条边， 因此，我们有 $P[\neg S_1] = 1-\frac{2}{n}$， 而 $S_2$ 在 $S_1$ 的前提下发生的概率为 $P[\neg S_2 | \neg S_1] = 1- \frac{2}{n-1}$。

因此，一次 Karger 操作，恰好得到最小割的概率为：

$$P[\neg S_1 \land \neg S_2 \land … \neg S_{n-2}] $$

$$= (1-\frac{2}{n})\times (1-\frac{2}{n-1}) \times (1 - \frac{2}{n-2}) \times …. \times (1-\frac{2}{n-(n-3)}) = \frac{2}{n(n-1)} \geq \frac{2}{n^2}$$

可以发现，一次 Karger 操作，恰好得到最小割的概率是很低的。为了提升得到 最小割的概率，我们的处理方法是 多次独立重复运行 Karger 算法，并记录得到的割的大小。当 重复次数达到一定数量时，得到最小割的概率就会非常高。

典型的重复次数 为 $Cn^2ln(n)$，此时，多次执行，一次都没有进行 min-cut 的概率为(note: $1+x < e^x$)：

$$P[not-min-cut] = (1-\frac{2}{n^2})^{C\cdot n^2 ln(n)} \leq e^{-2 C ln(n)} = \frac{1}{n^{2C}}$$

通过调整上面的常数 C，我们可使得无法得到 min-cut 的概率非常的小。即，通过多次的重复执行，Karger 算法得到正确 min-cut 的概率可以非常高。算法总的时间复杂度为 $O(n^4ln(n))$, (一次 Karger 操作的时间复杂度为 $O(n^2)$)，相比指数级的时间复杂度，得到了大大的优化。

Ref: http://web.stanford.edu/class/archive/cs/cs161/cs161.1166/lectures/lecture15.pdf