算法课程笔记-分治算法举例分析

发表于 分类于 ， Valine：

本文是系列算法课程的笔记，课程地址。前面一篇博客 介绍了主定理和几个分治算法的例子。这里再补充两个例子，并用代码对分治算法的实现进行说明。

1. 分治算法求解逆序数问题

在数组中，逆序数对是这样定义的：对于数组中的两个数字，如果前面一个数字大于后面一个数字，则称这两个数字形成一个逆序数对。例如，[7,5,6,4], 里面就有 5 对逆序数，为：{7,5}, {7,6}, {7,4}, {5,4}, {6,4}。

求解一个数组中的逆序数对，最简单的方法是暴力枚举所有的数对，看其中的 逆序数对的数量，时间复杂度为 O(n^2)。有没有方法可以提升算法的效率呢？答案是肯定的。我们可以使用 归并排序的方法对数组进行排序，在排序的过程中，统计 逆序数对的情况，从而将算法的时间复杂度降低为 O(nlogn)。

当然，想要借助归并排序实现 逆序数 的统计，我们首先需要搞清楚 二者的联系。这里我们关注一次归并的过程。如下图所示，归并排序的归并操作是将两个较短的有序的数组合并为一个更长的有序数组，在合并的过程中，我们使用 三个指针，分别指向 两个短的子数组的起始位置和 合并后的长数组的起始位置。进行合并时，我们比较 curLeft 和 curRight 指向的元素的大小，将较小的那个放置到 合并后数组中 cur 指向的位置，然后将 选中的数字所在子数组中的 cur 和 合并后数组中的 cur 分别向后移动一位。

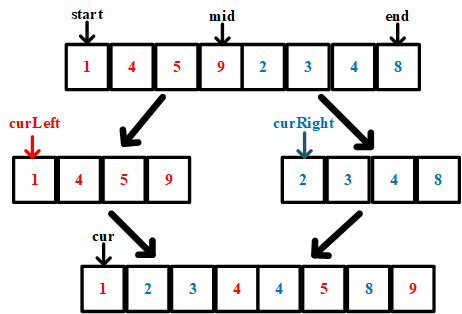
在移动的过程中，我们发现，当从 右半边添加数字到合并数组时，左半边数组中所有的数字与右半边该数字分别形成一个逆序数对。例如，当我们将右半边数组中的元素 “2” 放置到合并后数组中时，左半边数组中还剩余 3 个数字，分别是 4, 5, 9, 这三个数字分别和 2 形成一个逆序对。因此，我们可以总结规律，在归并的过程中，每当移动 curRight 的时候，则逆序对的数量需要添加 “左侧数组中剩余元素数量” 对。

这其中有需要注意的细节点是，如果左右指针指向的元素是相等的，则需要先放置左指针指向的元素，因为 逆序数的定义为 “前面一个数字大于后边一个数字”，而相等的两个元素不构成逆序数，因此，需要将 左边的元素先放置到合并数组中，从而当移动右指针时，不会统计到左侧数组中与右指针指向数字相等的元素。

使用 leetcode中的题目进行测试(link)，实现代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    int res = 0;
    public int reversePairs(int[] nums) {
        mergeAndCount(nums, 0, nums.length-1);
        return res;
    }

    // 归并排序并计算逆序对数
    void mergeAndCount(int[] nums, int start, int end) {
        // 边界条件，当待归并的数组长度为 0 或者 1 的时候，直接返回
        if(start >= end) return;
        int mid = start + (end - start) / 2;

        // 对数组左半边和右半边 分别排序
        mergeAndCount(nums, start, mid);
        mergeAndCount(nums, mid + 1, end);

        // 将两个有序的子数组合并为一个更长的数组
        merge(nums, start, mid, end);
    }

    void merge(int[] nums, int start, int mid, int end){
        // 新建一个数组用于放置 归并后的结果
        int[] mergeResult = new int[end-start+1];
        int curLeft = start, curRight = mid + 1;

        // 合并两个有序数组
        for(int cur = 0; cur < mergeResult.length; ++cur){
            // 分析移动左指针的情况：
            // 情况1：右指针超出了边界，直接移动左指针
            // 情况2：左指针和右指针都在界内，则如果 左指针指向的元素小于等于右指针指向的元素时，移动左指针
            if(curRight > end || (curLeft <= mid && nums[curLeft] <= nums[curRight])){
                mergeResult[cur] = nums[curLeft];
                curLeft += 1;
            }else{
                mergeResult[cur] = nums[curRight];
                curRight += 1;
                res += (mid - curLeft+1);
            }
        }
        
        // 将合并完成的数组 mergeResult 放回到原 nums 数组中
        for(int i = 0; i < mergeResult.length; ++i){
            nums[start+i] = mergeResult[i];
        }
    }
}

2. 矩阵乘法问题

Strassen 算法是用于计算矩阵乘法的一种方法。

对于传统的 矩阵相乘乘法，假设两个 $n * n$ 的矩阵，他们的每个位置计算的复杂度为 O(n), 总的矩阵乘法的时间复杂度为 $O(n^3)$。我们有没有办法提升它的效率呢？回忆之前的 整数乘法的分治实现，可以将 $O(n^2)$ 的时间复杂度，降低为 $O(nlogn)$。

首先，类似之前的 Karatsuba 乘法，我们也将矩阵拆分成 4 个子矩阵，进行相乘。计算 子矩阵相乘，总计需要计算 8 个子矩阵的乘法，如下图所示：

https://zhuanlan.zhihu.com/p/133330692

如果仅仅是这样的拆分，根据主定理，我们有 子问题个数 a = 8, 输入数据缩小的规模 b = 2(矩阵从 n*n 变为 (n/2) * (n/2)), 额外的操作所需的时间复杂度为 $O(n^2)$(矩阵相加操作的时间复杂度), 总的时间复杂度为 $O(n^{log_ba}) = O(n^3)$，算法的时间复杂度并没有降低。

想要降低复杂度，就需要进行类似 Karatsuba 算法的操作，减少子问题的个数。Strassen 算法提供了一种将子问题个数 由 8 个缩减为 7 个的方法，从而算法的时间复杂度可以降低为 $O(n^{log_ba}) = O(n^{2.8})$。具体如下图所示：

关于 Stassen 是如何想到 7 个参数来求解 8 个参数的，思考的大方向的确定其实不难，就是减少递归的分支数。但是如果仔细看 构造的 7 个参数，实际上是比较复杂的。那么是如何设计构造出这 7 个参数的呢？ 老师说这是一个开放式的问题，并没有标准的答案。我猜可能作者就是慢慢凑出来的吧，试凑法也是个重要方法呢！哈哈。