二分查找典型题-绝对差值和

发表于 分类于 ， Valine：

二分查找可以以 O(logn) 的时间复杂度完成查找，最典型的二分查找问题是在一个排序数组中，查找特定的值，返回其下标。实际中，二分查找问题有着很多的变形，这里以一道典型的题目展示二分查找的一些典型变化。

这里分析的题目是 leetcode 中的 1818. 绝对差值和, 题目的要求如下：

给你两个正整数数组 nums1 和 nums2，数组的长度都是 n 。

数组 nums1 和 nums2 的 绝对差值和 定义为所有 |nums1[i] - nums2[i]|（0 <= i < n）的 总和（下标从 0 开始）。

你可以选用 nums1 中的 任意一个 元素来替换 nums1 中的 至多 一个元素，以 最小化 绝对差值和。

在替换数组 nums1 中最多一个元素 之后 ，返回最小绝对差值和。因为答案可能很大，所以需要对 1e9 + 7 取余 后返回。

分析

上面的这道题目，允许在 nums1 中替换一个数字，来减小与 nums2 数组中对应元素之间的距离，以实现 绝对差值和 的最小化。初看来，这道题目有点无从入手，我们可以将问题进行分解，实际上要求总的绝对差值和 最小化，可以分解为求解 nums2 中的每一位元素，nums1 中与该元素的最小差值。然后将该差值与原差值比较，得到差值可以减少的最大值 - maximumReduction，从而 最小的绝对差值 就等于 原绝对差值和 减去 maximumReduction。

因此，问题可以转换为遍历数组 nums2 中的每个元素，寻找 nums1 中与对应元素最近的元素，并计算差值。标准的二分查找问题是查找等于对应值的元素，而与对应元素最近的元素该如何查找呢？实际上，这里可以将该问题分为两类来处理，与 元素 target 最近的元素有两种可能性，一种是 最近的元素小于等于 target，一种是大于等于 target。求解小于等于 target 的最右边元素 和 大于等于 target 的最左边元素的代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// 寻找小于等于 target 的最大值
int findFlooring(int[] nums, int target){
    int left = 0, right = nums.length-1;
    while(left < right){
        int mid = left + (right - left + 1) / 2;
        if(nums[mid] > target){
            right = mid - 1;
        }else{
            left = mid;
        }
    }
    return nums[left];
}

// 寻找大于等于 target 的最小值
int findCeiling(int[] nums, int target){
    int left = 0, right = nums.length-1;
    while(left < right){
        int mid = left + (right - left)/2;
        if(nums[mid] < target){
            left = mid + 1;
        }else{
            right = mid;
        }
    }
    return nums[left];
}

由于我们的查找一定有解，所以 while 中使用 < 而未用 <=。上述两个函数主要的不同之处在于 mid 值的选取，对于寻找 最大值 的 flooring 函数，mid 值是中间右偏的，这样，如果有相等的值，指针会不断的右移，从而找到的是 最右边的值。类似的，ceiliing 函数寻找的是最小值，mid 则是中间左偏。需要注意的是，findFlooring 返回的值不一定在 findCeiling 的左边，当 数组中有等于 target 的值时，findFlooring 最终的指针指向最右边的一个 target，而 findCeiling 最终的指针指向的是最左边的一个 target。如下图所示：

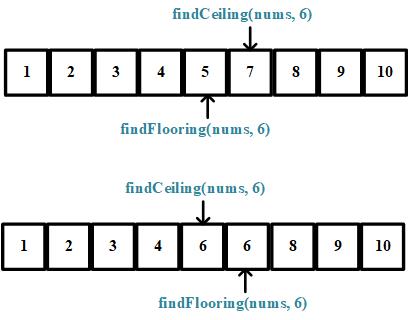
最后，如果数组中所有的元素都大于 target，findFlooring() 会返回数组中最左边的元素，类似的，如果都小于 target，findCeiling() 会返回数组中最右边的元素，都是最靠近 target 的元素。

完成上述两个函数后，最近的元素为 两个函数返回值中距离 target 更小的那一个。我们可以通过一个函数来实现这个功能：

1
2
3
4
5
int findClosest(int[] nums, int target){
    int leftClosest = findFlooring(nums, target);
    int rightClosest = findCeiling(nums, target);
    return Math.abs(leftClosest - target) < Math.abs(rightClosest - target) ? leftClosest : rightClosest;
}

完成上述准备工作后，原问题的处理就相对简单了。具体的主函数的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int minAbsoluteSumDiff(int[] nums1, int[] nums2) {
    int mod = (int)1e9+7;
    int[] sortedNums1 = nums1.clone();
    Arrays.sort(sortedNums1);
    long sum = 0, maximumReduction = 0;
    for (int i = 0; i < nums1.length; i++) {
        int a = nums1[i], b = nums2[i];
        if (a == b) continue;
        int x = Math.abs(a - b);
        sum += x;
        int closestDis = Math.abs(b - findClosest(sortedNums1, b));
        maximumReduction = Math.max(maximumReduction, x-closestDis);
    }
    return (int)((sum - maximumReduction) % mod);
}