leetcode 周赛中遇到的一道需要使用 字典树的题目,总结分析一下。
题目:查询最大基因差, 给你一棵 n 个节点的有根树,节点编号从 0 到 n - 1。每个节点的编号表示这个节点的 独一无二的基因值 (也就是说节点 x 的基因值为 x)。两个基因值的 基因差 是两者的 异或值 。给你整数数组 parents ,其中 parents[i] 是节点 i 的父节点。如果节点 x 是树的 根 ,那么 parents[x] == -1 。
给你查询数组 queries ,其中 queries[i] = [nodei, vali] 。对于查询 i ,请你找到 vali 和 pi 的 最大基因差 ,其中 pi 是节点 nodei 到根之间的任意节点(包含 nodei 和根节点)。更正式的,你想要最大化 vali XOR pi。
请你返回数组 ans ,其中 ans[i] 是第 i 个查询的答案。
分析
题目中,将结点之间的树形关系通过 parent 数组进行存储,对于该结构,我们可以从一个结点出发,非常方便的寻找到树的根部。因此,最简单的想法是,直接从 nodei 出发,遍历从 nodei 到根结点之间的所有结点,选取其中 与 vali 异或值最大的值作为查询的答案即可。该暴力解法代码如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public int[] maxGeneticDifference(int[] parents, int[][] queries) {
int[] res = new int[queries.length];
for(int i = 0; i < queries.length; ++i){
int[] query = queries[i];
int node = query[0];
int val = query[1];
while(node != -1){
res[i] = Math.max(res[i], val ^ node);
node = parents[node];
}
}
return res;
}
}
|
不出所料,暴力方法直接超过时间限制。那么如何降低算法的时间复杂度呢?
一般地,对于这种比较型的题目,降低时间复杂度的方法是 在遍历比较的过程中,保存前面比较的一些信息,用于后续 使用(例如 kmp 算法)。对于这里的树形结构,结点与它的父结点之间是有重复信息的,如下图所示, 结点 4 需要遍历 蓝色部分包围的 4 个结点,而其父节点需要遍历的结点与结点4 有3个结点为重复的。
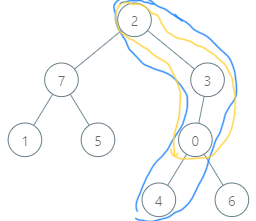
因此,一种想法是 使用 dfs 进行遍历,将遍历前序结点时的“信息“保存下来,后续结点只需要添加一些增加信息就可以进行判断。这里又有一个难点,就是该如何保存遍历到的结点的信息?字典树结构可以在这里派上用场。
具体地,我们使用字典树来保存结点的二进制信息,将一个数字保存到 字典树的过程如下:字典树以 root 为起点,待添加的数字从其二进制最高位开始依次向低位进行遍历,如果该位上数字为1,则 root 的左节点加1,并将左节点设置为新的 root;如果该位上数字为0,则root 的右结点加1,并将右结点设置为新的root。如下图所示。
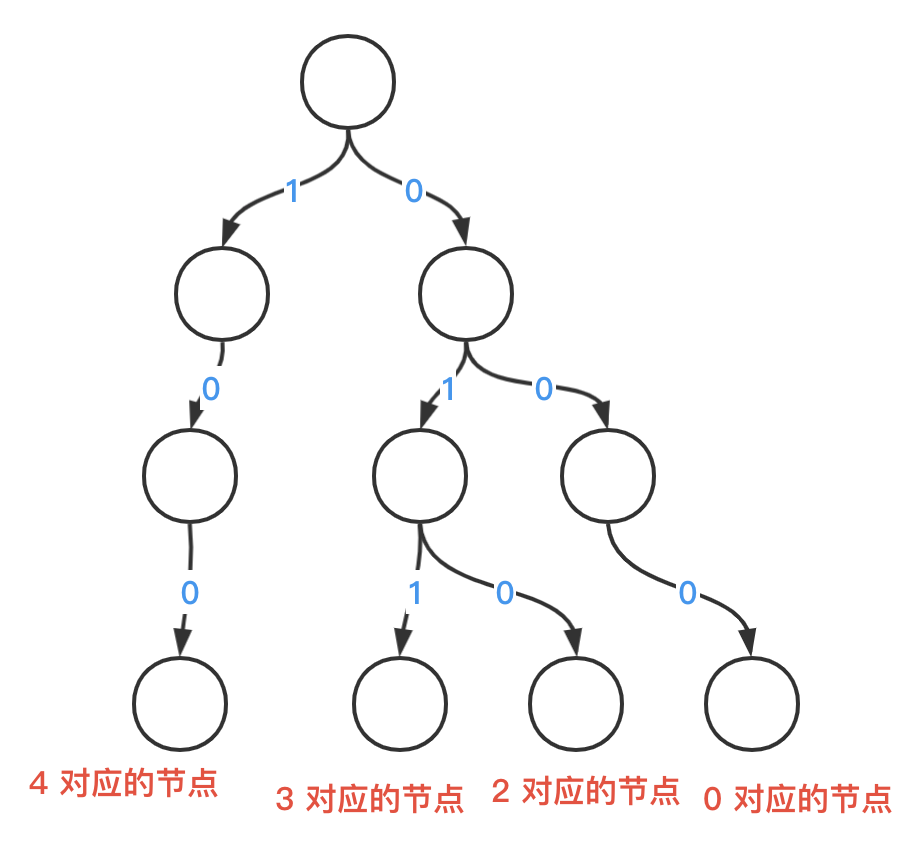
FigSource
将结点信息存放到树中之后,求解与特定 val 值异或结果的最大值就非常简单了,具体的,我们设异或结果的最大值为 res,遵循下面的规则确定各二进制位上的数字即可:
- 如果 val 当前二进制位上的值为 1:
- 若字典树中当前节点有 右子节点(有0),则 res 该位上为 1,root 结点变更为 右子结点;
- 若字典树中当前节点无 右子节点,res 该位上为 0,root 结点变更为 左子结点;
- 如果 val 当前二进制位上的值为 0:
- 若字典树中当前节点有 左子节点(有1),则 res 该位上为 1,root 结点变更为 左子节点;
- 若字典树中当前节点无 左子节点,res 该位上为 0,root 结点变更为 右子节点;
代码分析
整个的代码主要分为三个部分:
首先是将题目中给定的信息重新组织,将parent 数组表示的树结构转换为根结点引出子结点的结构,可以使用 map 存储,key 值为根结点值,value 为一个 list,存放根结点的叶子结点。但由于这里的 node 是从0到 n-1 的确定的值,我们也可以使用 数组来存放 树信息,数组下标为 node 的值,数组中的内容为该 node 的子结点。此外,对于查询,我们将针对相同 node 的查询汇总起来,同样放置到一个 map 中,key 值为 node 值,value 为一个list,放置针对该node 的查询。具体代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| class Solution {
int[] res;
public int[] maxGeneticDifference(int[] parents, int[][] queries) {
res = new int[queries.length];
int root = -1;
for(int i = 0; i < parents.length; ++i){
if(parents[i] == -1){
root = i;
break;
}
}
List<Integer>[] treeInfo = new ArrayList[parents.length];
for(int i = 0; i < treeInfo.length; ++i){
treeInfo[i] = new ArrayList<>();
}
for(int i = 0; i < parents.length; ++i){
int parent = parents[i];
if(parent == -1) continue;
treeInfo[parent].add(i);
}
Map<Integer, List<Integer>> queryMap = new HashMap<>();
for(int i = 0; i < queries.length; ++i){
int[] query = queries[i];
List<Integer> list = queryMap.getOrDefault(query[0], new ArrayList<>());
list.add(i);
queryMap.put(query[0], list);
}
TrieTree tt = new TrieTree();
dfs(treeInfo, queryMap, queries, tt, root);
return res;
}
void dfs(List<Integer>[] treeInfo, Map<Integer, List<Integer>> queryMap, int[][] queries,TrieTree tt, int root){
}
}
|
第二部分,是进行树的 dfs 遍历,具体就是以经典的递归方式实现使用程序栈进行遍历。需要注意的是,在遍历的过程中,有一个回溯的过程,因为当前结点仅和他的子结点们公用一些信息,而与其他的结点并不公用信息。因此,完成一个结点的所有子结点的遍历后,需要将该结点的信息从 trie tree 中删除。具体代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| void dfs(List<Integer>[] treeInfo, Map<Integer, List<Integer>> queryMap, int[][] queries,TrieTree tt, int root){
tt.insert(root);
if(queryMap.containsKey(root)){
for(Integer queryIndex : queryMap.get(root)){
int[] query = queries[queryIndex];
res[queryIndex] = tt.search(query[1]);
}
}
if(treeInfo[root] != null){
for(Integer node : treeInfo[root]){
dfs(treeInfo, queryMap, queries, tt, node);
}
}
tt.delete(root);
}
|
最后,就是实现一个 trie tree 来从二进制位的角度,将结点值进行存储。我们使用一个单独的类来封装这个结构,并且提供 insert 结点值,delete 结点值,以及查询目标值与当前存储的元素的最大异或值的函数 search。具体代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| class TrieTree {
TrieTree left = null;
TrieTree right = null;
TrieTree cur = this;
int count = 0;
public void insert(int val){
cur = this;
for(int i = 31; i >= 0; --i){
if(((val >> i) & 0x1) == 0x1){
if(cur.left == null) cur.left = new TrieTree();
cur = cur.left;
cur.count++;
}else{
if(cur.right == null) cur.right = new TrieTree();
cur = cur.right;
cur.count++;
}
}
}
public void delete(int val){
cur = this;
for(int i = 31; i >= 0; --i){
if(((val >> i) & 1) == 1){
cur = cur.left;
cur.count--;
}else{
cur = cur.right;
cur.count--;
}
}
}
public int search(int val){
cur = this;
int res = 0;
for(int i = 31; i >= 0; --i){
if(((val >> i) & 0x1) == 0x1){
if(cur.right != null && cur.right.count > 0){
res += (1 << i);
cur = cur.right;
}else{
cur = cur.left;
}
}else{
if(cur.left != null && cur.left.count > 0){
res += (1 << i);
cur = cur.left;
}else{
cur = cur.right;
}
}
}
return res;
}
}
|

