典型题分析-树形动态规划

发表于 更新于 分类于 ， Valine：

leetcode 周赛题 1916. 统计为蚁群构筑房间的不同顺序 比较有趣，需要使用 树形动态规划的方法进行解决。

题目如下：

你是一只蚂蚁，负责为蚁群构筑 n 间编号从 0 到 n-1 的新房间。给你一个 下标从 0 开始 且长度为 n 的整数数组 prevRoom 作为扩建计划。其中，prevRoom[i] 表示在构筑房间 i 之前，你必须先构筑房间 prevRoom[i]，并且这两个房间必须 直接 相连。房间 0 已经构筑完成，所以 prevRoom[0] = -1。扩建计划中还有一条硬性要求，在完成所有房间的构筑之后，从房间 0 可以访问到每个房间。

你一次只能构筑 一个 房间。你可以在 已经构筑好的 房间之间自由穿行，只要这些房间是 相连的 。如果房间 prevRoom[i] 已经构筑完成，那么你就可以构筑房间 i。

返回你构筑所有房间的 不同顺序的数目 。由于答案可能很大，请返回对 1e9 + 7取余 的结果。

解答

1. 核心思路

第一感觉，这道题目是一道排列相关的题目，在排列的过程中，需要遵从 prevRoom[] 数组中所规定的顺序。因此，前置房间的位置是确定的，总是在第一个，后面的房间则可以任意的排列。因此，我们可能想到排列公式：

对于有 $a_0$ 个物品0，$a_1$ 个物品1， …. , $a_{n-1}$ 个物品 $n-1$, 则将他们排成一排，方案数量为：

$$\frac{(a_0+a_1+.. +a_{n-1})!}{a_0!\cdot a_1!\cdot…a_{n-1}!}$$

这里，我们以题目中的示例为例子说明，输入 [-1,0,0,1,2]，我们以前置房间号为根，将输入数组画成树的结构，如下图：

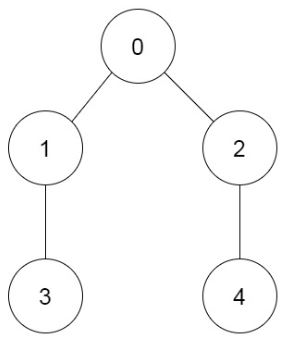
分析 0 号房间，它一共有 4 个子房间，分为两组，组内分别又有排序顺序规定。对于 0 号房间而言，在分析它时，我们就可以暂时先忽略 以 1号房 为根 和 以 4号房 为根的两组房间的内部顺序，即认为这些房间是无差别的相同房间，如上面解释中所说，“$a_0$ 个物品0”。

但实际上，“$a_0$ 个物品0”，这些物品是有差别的，内部亦有排列顺序要求。我们假设状态量 dp[k] 表示以第 k 个房间为根，该子房间组排列的方案数。房间 $u$ 为 房间 $v_1, v_2, …, v_m$ 的直接前置房间，有下面的关系式：

$$dp[u] = \frac{(size[u]-1)!}{\prod (size[v_i]!)}\cdot \prod dp[v_i]$$

上述关系式即为 动态规划的递推关系式。状态量 dp[k]为以房间 k 为前置房间，考虑其所有后继房间排列情况下的排列数量。从上面的递推关系式中，我们看到，递推时除了需要知道 dp[i] 值，还需要知道以 k 为前置房间时，所有的后继房间数量，因此，在程序编写中，还需要维护一个 size[i]记录以 房间i为前置房间总的房间数量，与 dp[] 数组同时更新。

此外，由于本题目是一个树形结构，通常需要使用递归的方法进行处理，即求解 dp[u] 时，需要递归调用求解函数，求解 dp[vi] 的值。终止递归的条件是当 dp[k] 不是任何房间的前置房间时，我们有 dp[k] = 1, size[k] = 1。

2. 求模问题

有了上述部分1的分析后，我们已经可以写出程序的整体框架。但是由于使用阶乘，答案的值可能很大，题目中要求我们给出模 1e9+7 的值。

对于乘法问题，求模相对简单，直接利用分配律即可。但对于除法问题，则不能直接利用分配律对分子和分母分别求模。因此，这里需要 引入求模意义下乘法逆元的概念。设模数为 m，对于一个整数，如果存在另一个整数 $a^{-1}$, 满足：

$$aa^{-1} \equiv 1(mod\ m)$$

则我们称，$a^{-1}$ 是a在求模运算下的 乘法逆元。通过逆元，我们可以将除法求模问题转换为乘法求模问题：

$$\frac{b}{a} \equiv b\cdot a^{-1} (mod\ m)$$

题目中，我们要求对 1e9+7 进行求模，我们知道该数字是一个质数。根据费马小定理，对于质数 m，且a 不是 m 的倍数（因为如果存在整数 $a^{-1}$, $aa^{-1}\equiv 1 (mod\ m)$, a 一定不是 m 的倍数）， 则有：$a^{m-1} \equiv 1 (mod\ m)$。根据该公式，我们可以快速的求得一个 $a^{-1}$ 的解 $a^{m-2}$。

对于原问题，我们遍历前置房间 u 的直接后继房间时，每次更新一个子房间 $v_i$，需要计算 $\frac{dp[v_i]}{size[v_i]!} \% (MOD)$ 的值，并将该值累乘到 dp[u]上。根据上面的分析，前面的除法求模可变为计算 $(dp[v_i] \% MOD) \times (size[v_i]!^{(m-2)} \% MOD)$ 。这里，分母部分的求模涉及到指数求模问题，可以使用快速幂求模法，进行求解（参考）。

3. 代码

根据上述分析，Java 代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
class Solution {
    /**
    * 参数：
    * fac: 放置 k! % MOD 的值，k 为数组下标值；
    * inv: 放置 k!^(MOD-2) % MOD 的值。也就是 k! 在求模意义下的逆元 k!^(-1) 模 MOD 的值。用于后面将除法运算化为乘法运算；
    * dp: 动态规划状态量，记录第 i 个房间为根结点时，可能的建筑顺序数量
    * size: 第 i 个房间为根结点时，整颗树包含的房间数量
    */
    final int MOD = 1_000_000_007;
    int[] fac, inv;  
    int[] dp, size;

    public int waysToBuildRooms(int[] prevRoom) {
        int n = prevRoom.length;
        dp = new int[n];
        size = new int[n];
        fac = new int[n];
        inv = new int[n];

        // 初始化 fac[] 和 inv[], 将计算好的阶乘值先存储在数组中，方便后续使用。
        fac[0] = inv[0] = 1;
        for(int i = 1; i < n; ++i){
            fac[i] = (int)((long)fac[i-1] * i % MOD);
            inv[i] = power(fac[i], MOD-2);
        }

        // 将 prevRoom[] 信息放置到 map 中，key 值为前置房屋的信息，value 值为以 key 房间为前置房间的房间号列表
        Map<Integer, List<Integer>> map = new HashMap<>();
        for(int i = 1; i < n; ++i){
            int prev = prevRoom[i];
            List<Integer> list = map.getOrDefault(prev, new ArrayList<>());
            list.add(i);
            map.put(prev, list);
        }

        dfs(map, 0);
        return dp[0];
    }

    // dfs(): 深度优先搜索，求解以 k 为起始房间的建筑顺序数量
    void dfs(Map<Integer, List<Integer>> map, int k){
        // 边界条件: 如果 map 中不含有 该房屋编号k，则说明这个房屋不是任何房屋的前置房屋。故 dp[k] = 1
        if(!map.containsKey(k)){
            dp[k] = 1;
            size[k] = 1;
            return;
        }
        List<Integer> list = map.get(k);
        dp[k] = 1;
        for(int cur : list){
            // 首先遍历所有子树
            dfs(map, cur);
            size[k] += size[cur];
            dp[k] =(int)((long)dp[k] * dp[cur] % MOD * inv[size[cur]] % MOD);
        }
        dp[k] =(int)((long)dp[k] * fac[size[k]] % MOD);
        size[k]++;
    }

    // 快速幂求解 a^e % MOD 的值
    int power(long a, int e){
        long ans = 1;
        while(e > 0){
            if((e & 1) == 1){
                ans = ans * a % MOD;
            }
            a = a * a % MOD;
            e = e >> 1;
        }
        return (int)ans;
    }
}