分治算法和主定理
分治是一个非常重要的算法思想,思路是通过将一个大的问题,分拆为多个同样类型,但是规模较小的子问题,从而进行递归求解。但需要注意的是,并不所有问题都可以通过分治的方法,降低其时间复杂度。本篇首先介绍了分析分治算法时间复杂度的方法:主定理,然后以几个典型的使用分治算法解决的问题作为例子,对分治算法进行进一步的说明。
1. 主定理(Master Method)
主定理是用于计算以递归方式实现的 分治算法 的复杂度的方法。可以认为它是一个分析 递归问题 时间复杂度的 黑盒子。
我们首先分析问题的背景要求,主要有如下三条:
- 所有的 分治子问题,问题的大小规模需要相等(e.g. 归并排序,数组的左半边和右半边的长度是相等的);
- 要求 满足边界条件,对于足够小的 n,$T(n)$ 的时间复杂度为常数级别;
- 对于所有的大 n,有关系式 $T(n) \leq aT(n/b) + O(n^d)$。
对于上面的第3点,参数 a, 是 子问题的个数,b 为输入数据规模缩小的因子,d 为除递归操作额外所需要的操作耗时(主要是 combine step 的耗时)。
在上述参数的前提下,$T(n)$ 可以分为下面三种情况:
- 当 $a = b^d$ 时,复杂度为:$O(n^d logn)$,
- 当 $a < b^d$ 时,复杂度为:$O(n^d)$,
- 当 $a > b^d$ 时,复杂度为:$O(n^{log_ba})$。
对于上述定理的证明,这里简单进行一下分析。我们首先思考,当 第 j 次递归的时候,我们需要进行的计算量为:
$$c\cdot n^d \times (\frac{a}{b^d})^j$$
c 是常数项。可以发现,第 j 次递归所需要的计算量正比于 $a$,反比于 $b^d$, 我们称 $a$ 为 子问题的增长速率 RSP(rate of subproblem proliferation),$b^d$ 为问题收缩的速率 RWS(rate of work shrinkage)。因此,根据 $a$ 与 $b^d$ 之间关系,有下面三种情况:
- 当 RSP == RWS 时,每一次递归处理的问题规模都是相同的,因此,实际算法复杂度取决于递归的层数,因而 $T(n) = O(n^dlog(n))$;
- 当 RSP < RWS 时,当递归层数增加,每层需要进行的工作变少, 因而算法复杂度约等于 $O(n^d)$;
- 当 RSP > RWS 时,当递归层数增加,每层需要进行的工作量增加,在叶子节点所在层次,所需要进行的计算量最大,因而复杂度应该约等于 叶子结点的数量 $O(\#leaves)$。($a^{log_bn} = n^{log_ba}$, - 欲证明二者相等,两边以b为底取对数即可)
2. 例子
2.1 乘法问题
对于最简单的两个 n 位数相乘问题,使用最朴素的乘法计算方法,时间复杂度是 $O(n^2)$。Karatsuba 乘法通过将问题进行拆分,并且用加减操作代替部分乘法操作,实现了算法时间复杂度的降低。算法的步骤如下图所示:
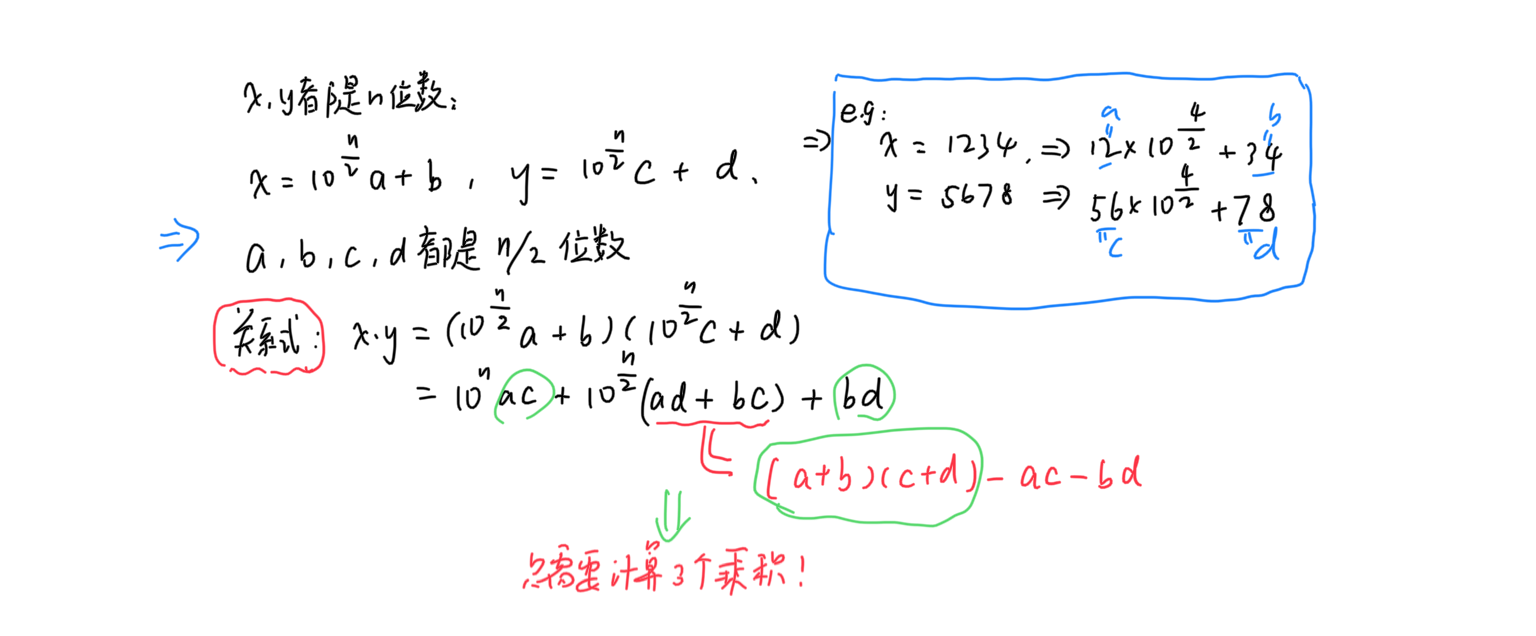
通过 上面红字部分的简化,算法的复杂度$T(n)$ 有如下关系:$T(n) = 3T(n/2) + O(n)$。对应到主定理中,$a = 3, b = 2, d = 1$, 因此算法的复杂度为:$O(n^{log_23}) \approx O(n^{1.58}) < O(n^2)$.
2.2 归并排序
归并排序是一个典型的分治算法。输入量为一个乱序的数组,输出则为排序后的数组。
思路很简单,三步:
- 排列数组的左半边,让左半边有序;
- 排列数组的右半边,让右半边有序;
- 将左右半边的数组合并为一个新的有序数组。
使用递归的方法进行编程,边界条件是当数组只有一个元素的时候,默认是有序的。此外,归并的时候,需要使用额外的空间,放置合并后的数组。
数组中的逆序对问题 可以在归并排序的同时进行分析,具体地,在归并的时候,当 将右半边数组中的元素放置到合并后的 序列中时,如果左半边数组中还有元素,则逆序对数增加 “当前左半边数组中元素个数” 个。
根据主定理,对于归并算法,$a = 2, b = 2, d = 1$, 所以算法的时间复杂度为 $O(nlogn)$。
2.3 最近点对问题(Closest Pair Problem)
问题:搜索一组点集中距离最近的两个点(点集为二维平面上的点集)。
最简单的方式是暴力搜索,算法时间复杂度时 $O(n^2)$。然而我们可以通过 分治的方法将算法的时间复杂度降低为 $O(nlogn)$。
算法的思路是将所有的点根据 x 坐标进行排序(同时 copy 一份按照 y 的坐标进行排序,后续需要使用),分治时,将 所有点根据 x 的坐标分成相等的两部分 $A_1$ 和 $A_2$,分界点为 $p_m (m = [\frac{n}{2}])$(向下取整)。
分治的过程就是:
- 求解左半边 $A_1$ 点集中的最短距离 d1;
- 求解右半边 $A_2$ 点集中的最短距离 d2;
- 求解 两个点集之间的最短距离(closet split pair)d3;
取上述三者中的最小值,即为最短距离。
上述过程中,核心难点是取两个点集之间的最短距离(即求解 splitPair)。这一步的具体做法是取 x 坐标为中间值的点 $p_m$ (点集 A1 最右边的点),以他的 x 坐标为中心点,左边和右边各拓展 $min(d1, d2)$ 的宽度,形成一个 宽度为 $2 * min(d1, d2)$ 条形区域 $S_y$。
然后,按照 y 坐标从小到大的顺序将 $S_y$ 区域中的点进行排序,最后依次 遍历 $S_y$ 中的点,每次分析时,比较 点 p 和 它后面的 7 个点,看他们的距离是否有小于 $\delta = min(d1, d2)$ 的。如果有,找到最小值,即为 该问题所寻找的最小距离。
为证明上述算法的正确性,我们证明下面两个辅助结论:
- 如果 p、q 为分属于两个点集且他们间的距离小于 $min(d1, d2)$,则 p、q 一定在 $S_y$ 中。
- p、q 为分属于两个点集的点,则按照 y 坐标排序,p、q 最多相差 7 个 位置。
上述结论 1 比较好证明。为说明结论2 的正确性,我们假设 $p = (x1, y1), q = (x2, y2)$ 为我们所寻找的分属于两个点集的最近点。假设 q 的y 坐标更小,我们以 q 的 y 坐标为下边界绘制下图,以 $\frac{\delta}{2}$ ($\delta = min(d1, d2)$)为边长,绘制 8 个小格子。
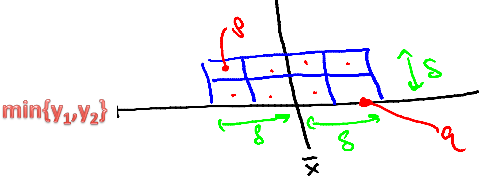
根据 p、q 分属于 两个点集以及 p、q 间的距离小于 $\delta$, 我们有下述结论:
- 所有$S_y$ 中的,并且 y 坐标在 p、q 之间的点,一定在上述的 8 个格子中。理由是 p、q 间的距离小于 $\delta$, 所以 p 的 y 坐标一定小于8个格子区域的上界。(也就是与 q 之间距离小于 $\delta$ 的点一定在上述 8 个格子中)
- 上述 8 个格子中,最多每个格子有 1 个点。通过反证法证明,如果一个格子中有两个点,则这两个点一定属于 同一个点集,并且 他们之间的距离最大为 $0.707 \delta$,小于 $\delta$。这与 $\delta = min(d1, d2)$ 相矛盾。
上述两个结论说明了,如果 p 与 q 之间的距离小于 $\delta$, 那么 p、q 按 y 坐标排序,二者之间最多相差 7 个元素。
复杂度分析:通过上述 ”最近7个点“ 的优化,我们将合并点集的算法复杂度降低为 $O(7n)$ 即 $O(n)$,因而有整体的算法复杂度 $T(n) = 2 * T(n/2) + O(n)$, 所以 $T(n) = O(nlog(n))$。
Remark:在程序设计中,有一些基础操作我们通常认为是 “for free” 的,即当你的数据可以放置到 memory 中,这些操作通常非常快,从而基本可以认为是 costless。排序, 通常被认为是这种 for free (or 成本很低的)的操作,我们可以随意调用。