非递归方法遍历二叉树

发表于 2021-02-05 更新于 2021-03-30 分类于 1- 编程相关，数据结构与算法阅读次数： Valine：

二叉树遍历是经典的算法题目，最传统的方案是使用递归的方式进行遍历，特点是代码非常简洁。当然，除了递归方案，二叉树也可以使用迭代的方法进行遍历。具体的，包括两种思路，一种是使用程序栈模拟递归过程，第二种是利用叶子结点的 null 子节点模拟线索二叉树完成遍历（Morries 方法）。本文将对他们进行总结归纳。

LeetCode 上三种遍历的题目如下，可以用来测试：

LeetCode前序遍历

LeetCode中序遍历

LeetCode后序遍历

1. 模拟递归栈解法

仔细分析二叉树遍历递归的过程，我们发现可以在迭代中使用 stack 来模拟系统栈，从而对递归进行模拟。

下面代码展示了 前序遍历 的过程：

public List<Integer> preorderTraversal(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    if(root == null) return res;
    
    Deque<TreeNode> stack = new ArrayDeque<>();
    stack.push(root);
    while(!stack.isEmpty()){
        TreeNode tmp = stack.pop();
        res.add(tmp.val);
        if(tmp.right != null) stack.push(tmp.right);    // 先push左节点，再push右节点
        if(tmp.left != null) stack.push(tmp.left);    
    }
    return res;
}

具体过程如下图所示：

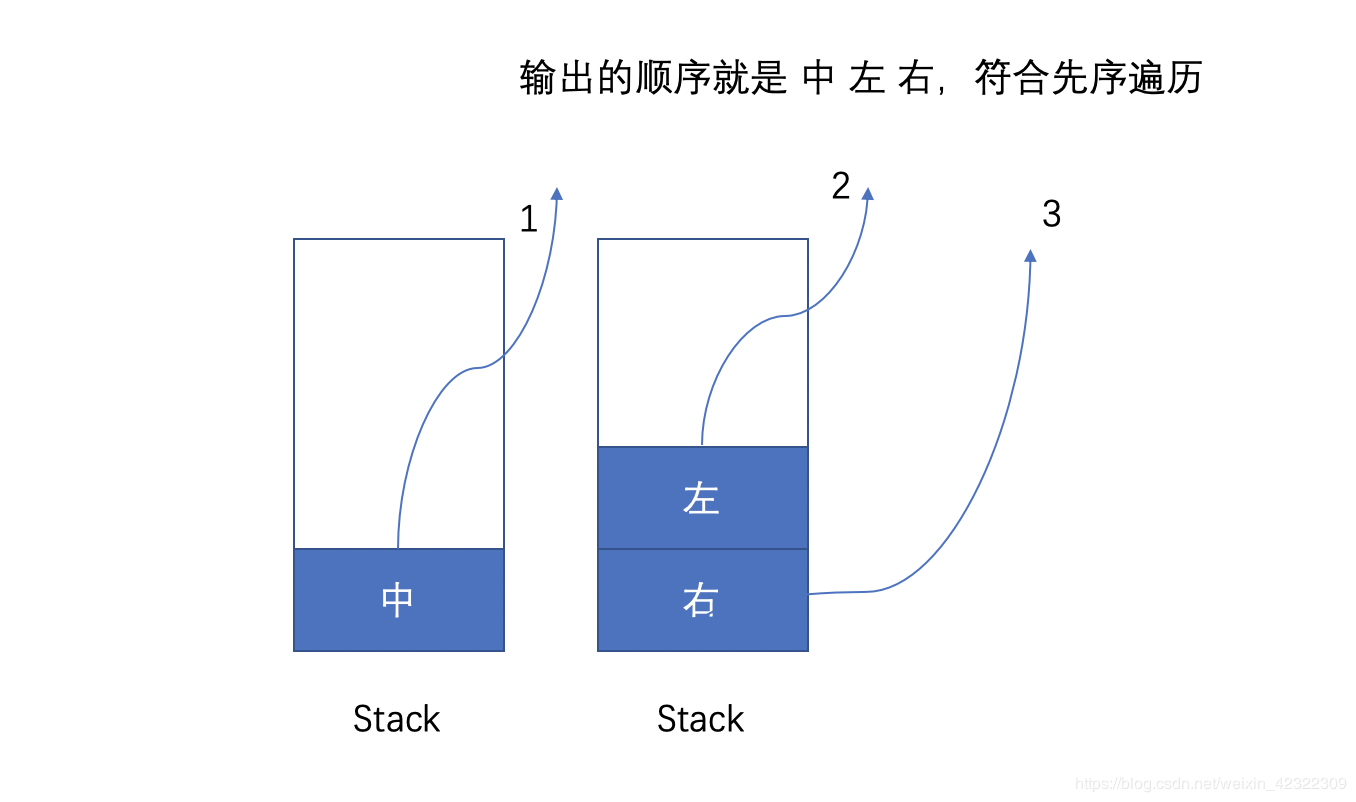
中序遍历 相对逻辑上复杂一些，它需要首先输入最右边的结点，因此，要保证最右边的结点位于栈顶。具体的流程参看下面的代码：

public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    if(root == null) return res;

    Deque<TreeNode> stack = new ArrayDeque<>();
    TreeNode cur = root;
    // 这里判断条件添加了一个 cur != null
    // 用于从左子树回溯到根，stack 中元素被 pop 完毕后，再遍历右子树
    while(!stack.isEmpty() || cur != null){    
        // 最左边元素全部压栈  
        while(cur != null){
            stack.push(cur);
            cur = cur.left;
        }
        // 将 pop 出来的结点暂存
        TreeNode tmp = stack.pop();
        res.add(tmp.val);
        // 遍历刚pop 出来结点的右子树
        if(tmp.right != null) cur = tmp.right;
    }
    return res;
}

后序遍历 后序遍历是先遍历完左右子树，最后回到根结点。这一点上其实和前序遍历有些类似 - 前序遍历是中左右的顺序，而后序遍历可以看作是 “中右左” 的反顺序。

具体代码如下：

public List<Integer> postorderTraversal(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    if(root == null) return res;
    Deque<TreeNode> stack1 = new ArrayDeque<>();    // 按 中右左 的顺序遍历-- 反过来就是后序遍历
    Deque<Integer> stack2 = new ArrayDeque<>();     // 使用 栈结构实现反序
    stack1.push(root);
    while(!stack1.isEmpty()){
        TreeNode tmp = stack1.pop();
        stack2.push(tmp.val);
        if(tmp.left != null) stack1.push(tmp.left);
        if(tmp.right != null) stack1.push(tmp.right);
    }

    res.addAll(stack2);
    return res;
}

上述方法中使用了两个栈，而另一种 后序遍历 则通过添加一个 cur 指针标记当前退出的结点，来减少一个栈的使用，因此更加推荐：

public List<Integer> postorderTraversal(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    if(root == null) return res;

    Deque<TreeNode> stack = new ArrayDeque<>(){{push(root);}};
    TreeNode cur = root;
    while(!stack.isEmpty()){
        // 当前的栈顶结点
        TreeNode peek = stack.peek();
        // step1: 先将最左侧结点全部压栈
        if(peek.left != null && peek.left != cur && peek.right != cur){
            stack.push(peek.left);
        }else if(peek.right != null && peek.right != cur){
            // step3: 处理右节点
            stack.push(peek.right);
        }else{
            // step2: 弹出最左侧结点，并将 cur 指向这个退出的结点
            cur = stack.pop();
            // step4: 弹出右节点，并将 cur 指向这个退出的结点
            res.add(cur.val);
        }
    }
    return res;
}

2. Morris 解法

不同于递归遍历和模拟栈遍历方法， Morris 遍历方法可以仅使用 O(1) 的空间复杂度对二叉树进行遍历。由于不能使用栈作为辅助空间，Morris 方法使用了线索二叉树 (threaded binary tree) 的概念来辅助树的遍历。当然，Morris 方法不需要为每个结点额外分配空间指向其前驱（predecessor）和后继（successor），而是利用叶子结点中的左右空指针来实现到后继结点的跳转。

Morris方法的中序和前序遍历较为简单，后序遍历则比较复杂。具体介绍如下：

中序遍历 首先以中序遍历为例子，介绍整个遍历思路。在遍历过程中，维护两个指针，cur1 指针为指向当前所遍历结点的指针， cur2 指针则用于寻找当前节点的中序遍历之前驱结点（参考线索二叉树的相关概念 – 具体就是左子树中的最右边的结点）。

初始状态：cur1 指向根结点。

然后只要 cur1 不为空，就继续遍历，遍历过程如下：

若 cur1 的左孩子为空：处理当前节点，cur1 指向 cur1.right。
若 cur1 的左孩子不为空，则使用 cur2 找到 cur1 中序遍历的前驱结点（即左子树的最右边的结点）：
- 若 cur2 的右孩子为空，则将 cur2 的右孩子设为 cur1 – 建立连接。然后 cur1 指向 cur1.left;
- 若 cur2 的右孩子不为空（为 cur1），说明当前 cur1 的右孩子已经全部遍历完成，将 cur2 的右孩子恢复为 null。再处理 cur1，并将 cur1 指向 cur1.right。

具体参考下方代码：

public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    if (root == null) return res;

    TreeNode cur1 = root;   // 指向当前遍历到的结点
    TreeNode cur2 = null;   // 寻找当前遍历到的结点的 前驱结点

    while (cur1 != null) {
        cur2 = cur1.left;
        //构建 前驱结点到当前节点的 连接
        if (cur2 != null) {
            // 一直向右寻找，找到最右边的结点
            while (cur2.right != null && cur2.right != cur1) cur2 = cur2.right;

            // 两种情况：
            // 情况1：前驱结点右孩子为空，将该有孩子设为当前遍历节点 cur1，建立连接 
            // 建立连接后，调整 cur1 指针，指向 cur1.left
            // 情况2：前驱结点右孩子 为cur1，说明该结点的左子树已经遍历完，恢复前驱结点
            if (cur2.right == null) {
                cur2.right = cur1;
                cur1 = cur1.left;
                continue;
            } else cur2.right = null;
        }
        res.add(cur1.val);
        cur1 = cur1.right;
    }
    return res;
}

前序遍历 前序遍历基本借鉴了中序遍历的思路，不同点有二：

在 cur2.right == null 时，不仅建立连接，还同时处理结点。

在中序遍历中，如果 cur1 结点左子树全部遍历完毕，则添加 cur1 结点的 val。前序遍历只有在 cur1 左子树为空的情况才添加 cur1.val。即前序遍历 if(cur2 != null){....}else res.add(cur1.val); 而中序遍历中，不需要添加 else。

public List<Integer> preorderTraversal(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    if(root == null) return res;
    TreeNode cur1 = root;
    TreeNode cur2 = null;

    while(cur1 != null){
        cur2 = cur1.left;
        if(cur2 != null){
            // 寻找左子树的最右边的结点 -- cur1 中序遍历的前驱结点
            while(cur2.right != null && cur2.right != cur1) cur2 = cur2.right;
            // 若 cur2.right 为 null： 添加 cur2 到当前节点的连接并且 处理 cur1 结点
            if(cur2.right == null){
                cur2.right = cur1;
                res.add(cur1.val);
                cur1 = cur1.left;
                continue;
            // 若 cur2.right 不为 null，恢复它为 null
            } else cur2.right = null;
        // 如果 cur1 左子树为空，直接处理 cur1
        }else res.add(cur1.val);
        cur1 = cur1.right;
    } 
    return res;
}

后序遍历 后序遍历相对复杂。前面的准备工作与前序、中序比较类似，但遍历输出时，需要进行的改动较大。

如下图所示，后序遍历时将结点的连续右节点当成一个单链表来看待。当cur 返回上层时，我们 逆序处理 下层的单链表。例如，返回到 2 时, 处理链表 4 (该链表只有一个结点)；返回到 1 时，处理链表 5 -> 2 。

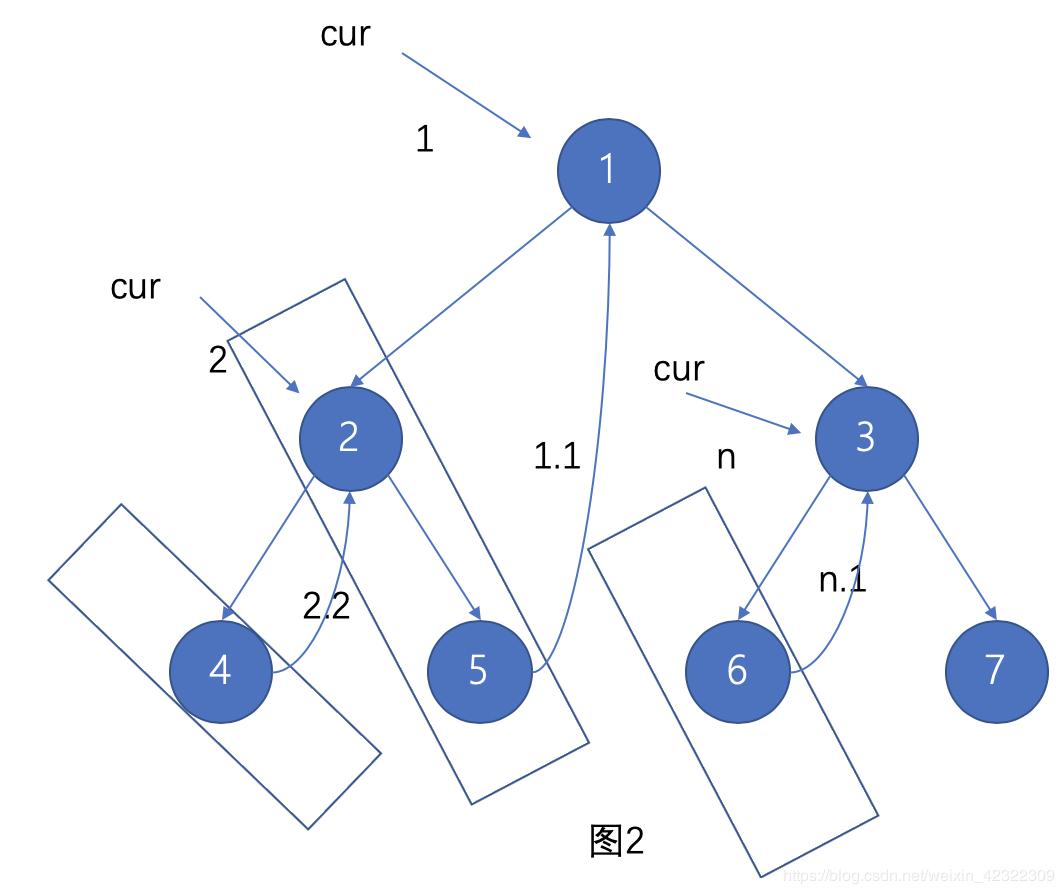
//后序Morris
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root == null) return res;
        TreeNode cur1 = root;   // 遍历时的指针变量
        TreeNode cur2 = null;   // 当前节点的中序直接前驱结点 -- 当前结点左子树的最右结点
        while(cur1 != null){
            cur2 = cur1.left;
            if(cur2 != null){
                while(cur2.right != null && cur2.right != cur1) cur2 = cur2.right;
                if(cur2.right == null){
                    cur2.right = cur1;
                    cur1 = cur1.left;
                    continue;
                }else{
                    cur2.right = null;
                    res.addAll(reverseList(cur1.left)); // 链表反序后加入 list
                }
            }
            cur1 = cur1.right;
        }
        res.addAll(reverseList(root));
        return res;
    }

    // 翻转单链表
    Deque<Integer> reverseList(TreeNode root){
        Deque<Integer> stack = new ArrayDeque<>();  // 使用 stack 来反序
        if(root != null) stack.push(root.val);
        while((root = root.right) != null) stack.push(root.val);
        return stack;
    }
}

参考:

[1] https://www.cnblogs.com/anniekim/archive/2013/06/15/morristraversal.html
[2] https://zhuanlan.zhihu.com/p/101321696
[3] https://leetcode-cn.com/problems/binary-tree-preorder-traversal/solution/leetcodesuan-fa-xiu-lian-dong-hua-yan-shi-xbian-2/
[4] https://leetcode-cn.com/problems/binary-tree-preorder-traversal/solution/tu-jie-er-cha-shu-de-si-chong-bian-li-by-z1m/