有限状态自动机

发表于 更新于 分类于 ， Valine：

有限状态自动机（FSM- Finite State Machine，又称为 Finite-State Automation，下面简称为 自动机），是表示有限个状态以及这些状态之间的转移和动作行为的数学计算模型。

自动机在计算科学，电子硬件编程 (e.g.FPGA) 等领域被广泛运用。

1. 有限状态机基础

对于自动机，它有下列几个要素 Ref：

  1. 状态- states；
  2. 输入- inputs；
  3. 输出- output；
  4. 转移规则- transition rules；
  5. 输出规则- output rules。

总结来说，它是一种顺序（sequential）进行的计算模型，它的每一个跳转动作由 当前状态、输入 和 转移规则 决定。此外，自动机还有两个特殊状态，分别为 起始状态 和 终止状态。

2. 使用 FSM 思想理解 KMP 算法

对于著名的 KMP 算法，在确定模式串的指针跳转方式时，就可以使用 自动机的思想来分析。

在 KMP 算法中，使用两个指针来确定主串和模式串的下一个比较字符，主串指针很简单，只需要每次移动一位，一直向前移动即可。而模式串的匹配指针移动则较为复杂。

下图中，通过自动机的方法，给出了模式串指针指针跳转的机制-使用自动机的语言来将，就是状态与状态之间的转移规则。

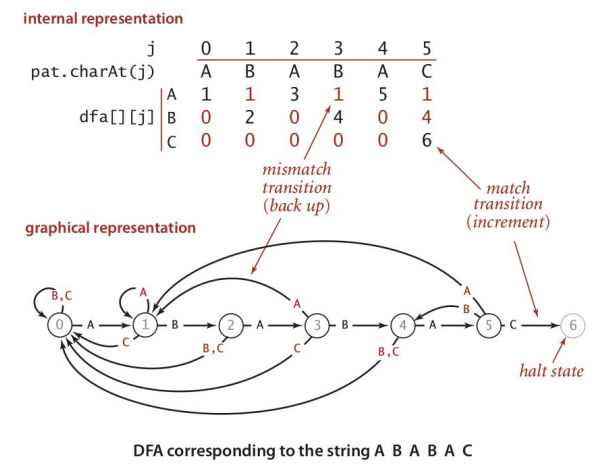
这里对上图进行具体的解释：

状态：图中共有6个状态，具体表示从字符串头开始，当前已经匹配到的字符数。

输入：这里用字符c 指代，实际上就是当前主串指针指向的字符。

转移规则，转移规则分为匹配和不匹配两种情况，如下：

  • 匹配：当状态 j 的时候，有 c == pat.charAt(j) 转移到 j + 1 状态；
  • 不匹配：状态 j 的时候，c != pat.charAt(j)，则将字串的 pat[1, j-1] + c (即模式串去除首字符的前 j 个字符，加上输入的字符 c 构成的字串) 放入自动机中，最终输出的跳转状态即为状态 j 时输入 c 的跳转状态。

解释1：不匹配时的转移规则：当状态 j 的时候，输入与模式串的第 j + 1 个字符不匹配，则需要确认 pat[0, j-1] + c 构成的字串的后缀子串中，有没有与 pat[0, j-1] 前缀子串完全匹配的。这时候，我们认为到 pat[0, j-1] 部分的状态都具有了完整的转移规则。

因此，我们将 字串的 pat[1, j-1] + c （长度与 pat[0, j-1] 相同）放入自动机中，一定可以获得一个完整的、确定的转移状态，我们记为 X'。此时，如果 字串 pat[1, j-1] + c 的某个后缀子串与 pat[0, j-1] 的一个前缀子串相同，则 X' 就是这个前缀子串完全输入后最终的转移到的状态。

Trick：在实际操作中，在每一步状态转移的同时，我们会保存模式串从 位置1到当前状态对应字符 这区间的子串 放入自动机的转移情况，即在状态 j 时，我们同时存储 pat[1, j-1] 输入状态机的最终转移状态（记为状态 X），从而提升遇到非匹配情况时的转移效率。

解释2：关于在模式串中未出现的字符：上述状态机中没有涉及输入遇到模式串中没有的字符的情况，其实可以在上述 dfa 数组中添加一行 “其他字符”，处理也很简单，全部填入 0 即可。因为如果遇到了模式串中不存在的字符，上述 不匹配时的转移规则 中提到的前后缀子串匹配的情况就不可能出现（因pat[0, j-1] + c 中 c 字符没有在 模式串中出现）。

参考文档：

  1. 中文博客-状态机和KMP算法
  2. MIT-tutorial on Knuth-Morris-Pratt Algorithm
  3. 使用fsa理解KMP-视频讲解-from coursera

此外，用 “部分匹配表” 方法处理 KMP 模式串的指针跳转：

  1. 字符串匹配的KMP算法-阮一峰的博客
  2. MIT-slides-Linear Time String Matching

3. 例子: 表示数值的字符串

LeetCode-表示数值的字符串

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。例如，字符串 "+100"、"5e2"、"-123"、"3.1416"、"-1E-16"、"0123" 都表示数值，但 "12e"、"1a3.14"、"1.2.3"、"+-5"及"12e+5.4" 都不是。

思路：使用自动机的思想来处理。编写代码之前，我们首先需要确立状态量和 状态量之间的转移规则。

状态量：我们将字符串按照数值量的组成部分进行划分：

  1. 起始的空格
  2. 符号位
  3. 整数部分
  4. 左侧有整数的小数点
  5. 左侧无整数的小数点（根据前面的第二条额外规则，需要对左侧有无整数的两种小数点做区分）
  6. 小数部分
  7. 字符 e
  8. 指数部分的符号位
  9. 指数部分的整数部分
  10. 末尾的空格

当前处理到的部分称为当前的状态（比较：前面kmp部分的状态是当前匹配到的字符的数量），输入量则为输入字符串中下一个遍历到的字符。

上述状态中，「初始状态」应当为状态 1，而「接受状态」的集合则为状态 3、状态 4、状态 6、状态 9 以及状态 10。

在下述情况下输出 false:

  1. 接收到的输入 无法使得当前状态转移到任何一个确定的状态；
  2. 字符串遍历完毕，但停留状态不是 接受状态。

具体的转移规则参看下方状态转移图（其中少了一根线，起始空格可以转移到整数部分）：

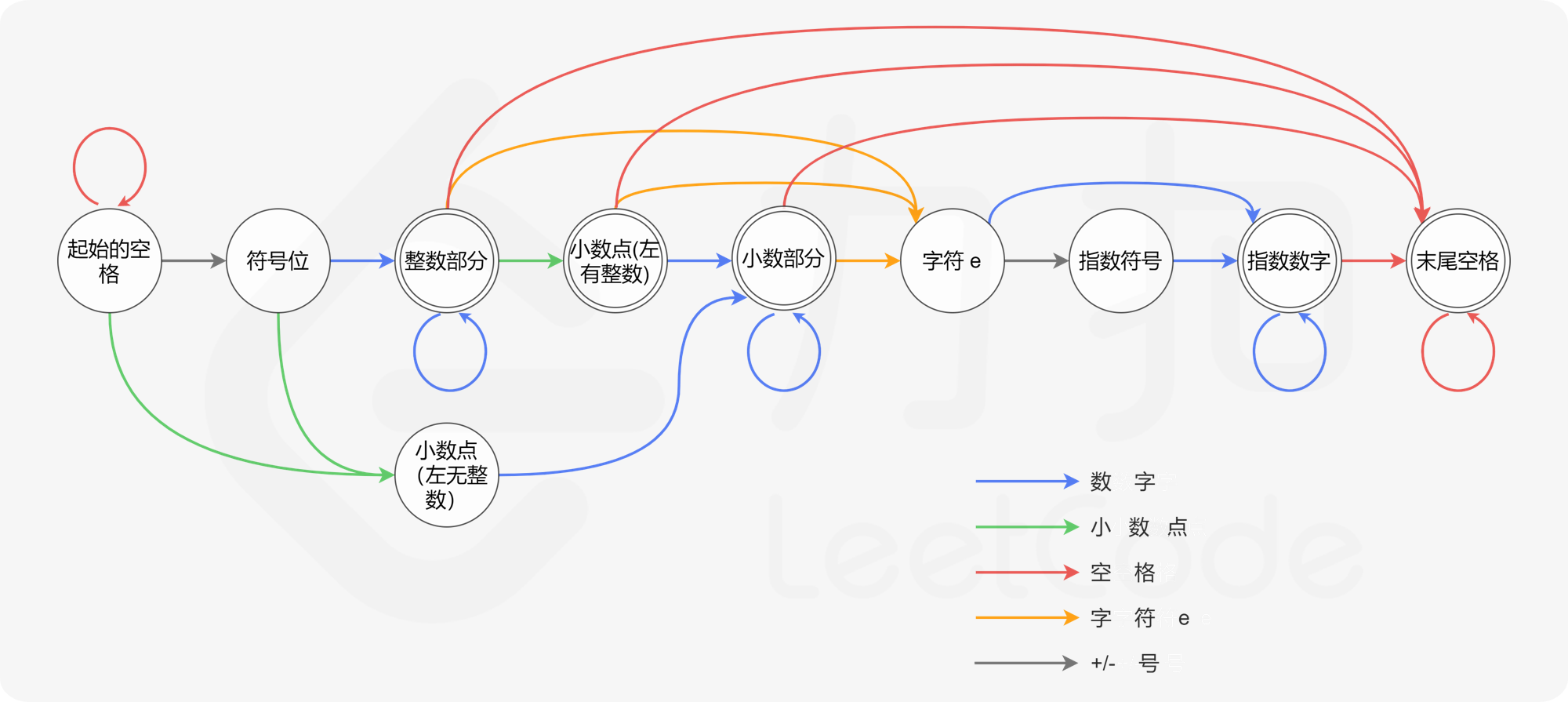
根据上方的状态以及状态转移规则，我们可以编写程序，在编写的程序中，我们使用 Map 存储状态转移规则。 下面的代码为Leetcode 官方题解(添加部分注释及少量修改)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
// annotations added by Matt
class Solution {
    private Map<State, Map<CharType, State>> transfer;
    public boolean isNumber(String s) {
        initialization();
        int length = s.length();
        State state = State.STATE_INITIAL;

        // 遍历字符串
        for (int i = 0; i < length; i++) {
            CharType type = toCharType(s.charAt(i));
            if (!transfer.get(state).containsKey(type)) {
                return false;
            } else {
                state = transfer.get(state).get(type);
            }
        }
        return state == State.STATE_INTEGER 
        || state == State.STATE_POINT 
        || state == State.STATE_FRACTION 
        || state == State.STATE_EXP_NUMBER 
        || state == State.STATE_END;
    }

    private void initialization(){
        // transfer 存储状态转移规则。状态转移需要：当前状态，输入量，输出状态
        transfer = new HashMap<State, Map<CharType, State>>();

        // 状态：初始空格
        Map<CharType, State> initialMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_SPACE, State.STATE_INITIAL);
            put(CharType.CHAR_NUMBER, State.STATE_INTEGER);
            put(CharType.CHAR_POINT, State.STATE_POINT_WITHOUT_INT);
            put(CharType.CHAR_SIGN, State.STATE_INT_SIGN);
        }};
        transfer.put(State.STATE_INITIAL, initialMap);

        // 状态：符号位
        Map<CharType, State> intSignMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_INTEGER);
            put(CharType.CHAR_POINT, State.STATE_POINT_WITHOUT_INT);
        }};
        transfer.put(State.STATE_INT_SIGN, intSignMap);

        // 状态：整数部分
        Map<CharType, State> integerMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_INTEGER);
            put(CharType.CHAR_EXP, State.STATE_EXP);
            put(CharType.CHAR_POINT, State.STATE_POINT);
            put(CharType.CHAR_SPACE, State.STATE_END);
        }};
        transfer.put(State.STATE_INTEGER, integerMap);

        // 状态：小数点（左有整数）
        Map<CharType, State> pointMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_FRACTION);
            put(CharType.CHAR_EXP, State.STATE_EXP);
            put(CharType.CHAR_SPACE, State.STATE_END);
        }};
        transfer.put(State.STATE_POINT, pointMap);

        // 状态：小数点（左无整数）
        Map<CharType, State> pointWithoutIntMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_FRACTION);
        }};
        transfer.put(State.STATE_POINT_WITHOUT_INT, pointWithoutIntMap);

        // 状态：小数部分
        Map<CharType, State> fractionMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_FRACTION);
            put(CharType.CHAR_EXP, State.STATE_EXP);
            put(CharType.CHAR_SPACE, State.STATE_END);
        }};
        transfer.put(State.STATE_FRACTION, fractionMap);

        // 状态：e 字符
        Map<CharType, State> expMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER);
            put(CharType.CHAR_SIGN, State.STATE_EXP_SIGN);
        }};
        transfer.put(State.STATE_EXP, expMap);

        // 状态：指数符号
        Map<CharType, State> expSignMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER);
        }};
        transfer.put(State.STATE_EXP_SIGN, expSignMap);

        // 状态：指数部分数字
        Map<CharType, State> expNumberMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_NUMBER, State.STATE_EXP_NUMBER);
            put(CharType.CHAR_SPACE, State.STATE_END);
        }};
        transfer.put(State.STATE_EXP_NUMBER, expNumberMap);

        // 状态： 结尾空格
        Map<CharType, State> endMap = new HashMap<CharType, State>() {{
            put(CharType.CHAR_SPACE, State.STATE_END);
        }};
        transfer.put(State.STATE_END, endMap);
    }

    // 判断输入的字符类型
    public CharType toCharType(char ch) {
        if (ch >= '0' && ch <= '9') {
            return CharType.CHAR_NUMBER;
        } else if (ch == 'e' || ch == 'E') {
            return CharType.CHAR_EXP;
        } else if (ch == '.') {
            return CharType.CHAR_POINT;
        } else if (ch == '+' || ch == '-') {
            return CharType.CHAR_SIGN;
        } else if (ch == ' ') {
            return CharType.CHAR_SPACE;
        } else {
            return CharType.CHAR_ILLEGAL;
        }
    }

    // 状态量
    enum State {
        STATE_INITIAL,
        STATE_INT_SIGN,
        STATE_INTEGER,
        STATE_POINT,
        STATE_POINT_WITHOUT_INT,
        STATE_FRACTION,
        STATE_EXP,
        STATE_EXP_SIGN,
        STATE_EXP_NUMBER,
        STATE_END,
    }

    // 输入的字符类型
    enum CharType {
        CHAR_NUMBER,
        CHAR_EXP,
        CHAR_POINT,
        CHAR_SIGN,
        CHAR_SPACE,
        CHAR_ILLEGAL,
    }
}