大话数据结构15-总结
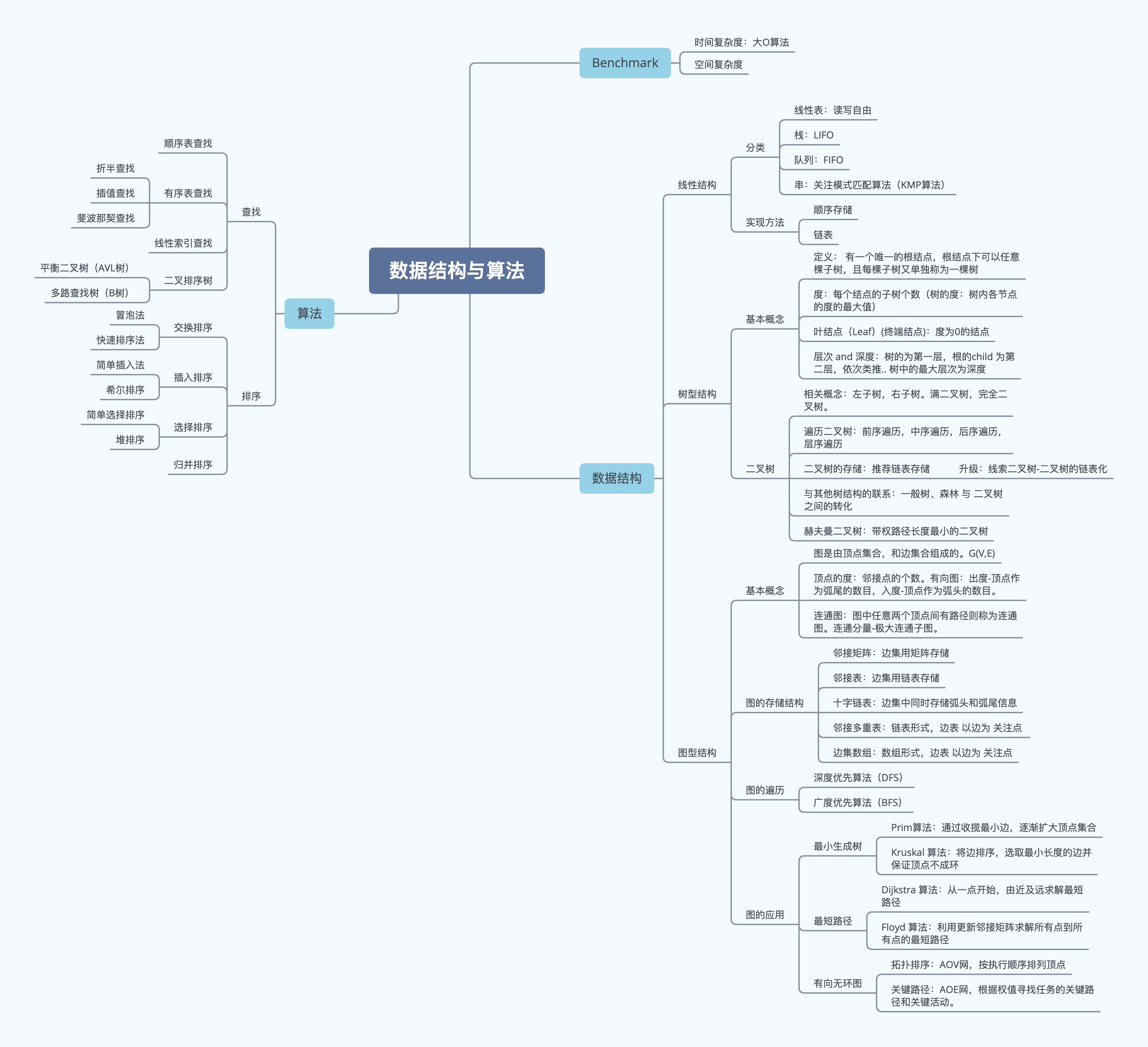
上两周,读完了《大话数据结构》这本书。记录了14篇学习文档。这里,首先,我将每章中觉得重要的内容在这里做一下总结,然后,在总结的基础上,脱离细节,做一下宏观上的分析,最后,以思维导图的形式,做一个汇总。
I. 算法与数据结构
a. 数据结构部分
Chap1-时间复杂度: 核心内容是算法的时间复杂度的分析,也就是大 O 算法。分析算法的 大O 复杂度其实不难,因为只需要关注最主要的高次项的影响,低次项可以简单的忽略处理。此外,要记住 大O算法 复杂度的排序。
$$O(log(n))< O(n)< O(nlog(n))< O(n^2)$$
Chap2-顺序存储结构: 顺序表结构也就是数组结构,它是一种读写方便,增删麻烦的存储结构。对于C语言来说,一定要非常关心数组的溢出问题。(Java 语言有自动的边界检查机制,似乎不存在这样的问题 refLink )
Chap3-链表: 链表是一种链式的存储结构,通过让每个存储元素都拥有数据域和指向下个元素的地址域,它不再要求数据在连续的物理空间上存储。它的好处是增删方便,但缺点是读写不便。
需要注意的概念是头指针和头结点,头结点是为了方便(使得增删操作更加一致),链表中常常添加的一个额外结点,它的数据域为空或存储链表相关信息(例如链表长度),它的地址域则指向链表第一个数据结点。而头指针则是指向链表的第一个结点-如果链表有头结点,则指向头结点,如果没有头结点,则指向第一个数据结点。
Chap4-栈: 栈是一种特殊的线性表,它的特点是 “后进先出”(LIFO)。栈的应用很多,例如对于递归类型的程序,就是通过栈来进行操作:最外层的递归程序先进栈,但最后执行。
Chap5-队列: 队列是一种特殊的线性表,它的特点是只允许在一端进行插入操作,在另一端进行删除操作。简单讲,就是“先进先出”(FIFO)。同样的,队列可以使用 数组 或 链表 进行存储。用数组存储时,为提升效率,需要使用循环队列结构。
Chap6-串: 即 String,核心内容是 String 的模式匹配算法。其中较为高级的叫做 KMP 算法,它的核心思想是减少重复的比对,具体包括:1-主串中指示比较进行的 index 不回退;2- 子串中指示的 index 根据一个生成的 next 数组作为 “比较指针” 跳动的依据。
Chap7-树: 树是一种一对多的数据结构,每个节点可以有多个子结点,但最多只能有一个 parent 结点(根结点无parent)。
核心内容是对二叉树(Binary Tree,度最大为2的树)的分析。首先是它的 遍历(及生成)方法,分为前序、中序、后序三种递归遍历方法,以及层序遍历法。线索二叉树 - 二叉树的链表化。 赫夫曼树 - 最优二叉树,带权路径长度(WPL)最小的二叉树,生成方法是:重复进行将最小的权值的两个结点合并的操作。
Chap8-图: 图是一种多对多的数据结构,实际上可以看作是两个集合:1- vertex 的集合,2- edge 的集合。图可以分为有向图和无向图。根据图中任两点间是否有 path,定义连通图。
图的存储核心是边的存储,因为边 涉及到两 顶点之间的关系。按照存储所使用的存储空间结构(顺序表or链表)引出最基础的两种存储方式:邻接矩阵(2阶矩阵) 和 邻接表 存储。进一步的,邻接表针对有向图的升级为 十字链表- 链表结点同时存储弧头和弧尾信息。更换另一种思路,以边为核心进行存储,有 数组形式的- 边集数组 和 链表形式的 邻接多重表。
图的遍历(traverse)分为深度优先算法(类似树的前序算法)和广度优先算法(类似树的层序遍历算法)。
连通网的 最小生成树(n个顶点,n-1条边),常用的有 Prim算法(逐步扩大顶点集合) 和 Kruskal算法(逐步扩大边集合)。
图中两点间的 最短路径,常用的有 Dijkstra算法(由近及远查找源点 到每个点的最短路径) 和 Floyd算法(宏观地对邻接矩阵进行演化)。
有向无环图的应用包括 AOV网的拓扑排序,及 AOE网 的关键路径查找。
b. 算法部分
Chap9-查找: 查找可以分为下面几类:
- 顺序表查找;(时间复杂度为$O(n)$.)
- 有序表查找;(折半查找,插值查找,斐波那契查找..不同的是查找时的划分点不同)
- 线性索引查找;(数据量大时,建立索引表来查数据。)
- 二叉排序树;(二叉排序树的中序遍历序列,就是从小到大的排序序列。)
- 平衡二叉树(AVL树);(平衡的二叉树查找效率最高)
- 多路查找树(B树);(每个结点可以存储多个元素,include:2-3树,2-3-4树 ..)
- 散列表(哈希表)查找。(重点是散列函数的构造和处理散列冲突的方法。)
Chap10-排序: 排序算法大致可以分为如下几类:
- 交换排序
- 冒泡法,遍历比较,通过交换,将小数“冒泡” or 大数“沉底”。
- 升级版:快排,分治处理,每组选择一个 pivot 值,将小于它的值放在数组前方,大于的放在后方。
- 插入排序
- 从数组最前端开始,通过插入数据,增长数组,直到遍历完毕。具体的,插入就是从待插入数组尾开始遍历,遍历的元素如果比待插入数据大,就向后移动一位,直到找到所关注的数据的待插入的位置为止。
- 希尔排序:分治法,按等距k 将数组分为 n/k 组,每一组施行插入排序。
- 选择排序
- 简单选择,首先寻找整个数组中最小的数,放在数组第一个,然后寻找次小的,放在第二个,… 直到外循环遍历完整个数组。
- 堆排序:设计了一个堆结构(一种二叉树),更容易的找出数组中的最大/最小元素。
- 归并排序。-分治思想。
最后,关于排序算法的稳定性,不是指时间复杂度的变化小,而是指 大小相同的元素 的顺序 是否与原数组中顺序相同。
c. 总结
回顾整本书,作者按顺序介绍了3种大的数据结构:线性表;树;图。每一种结构,都有很多分类,变形。例如线性表,包括队列,栈。此外,数据在计算机中的存储空间是否连续,决定了数据结构以数组还是链表的形式存储,最终又产生了很多的分支和细节的内容。
介绍完数据结构之后,是算法的介绍。所谓算法,其实就是寻找高效的数据查找、数据排序的方法。从算法的介绍中,我们可以发现,之所以数据结构与算法连在一起讲,是因为算法性能的提升,常常需要依赖于特定的数据结构。例如排序二叉树,就是利用了二叉树的特性,将算法的思想,与数据在计算机中的实际存储结构相结合联系。最终达到提高效率的目的。