大话数据结构14-排序2

发表于 更新于 分类于 ， Valine：

前面我们介绍了相对基础的 冒泡排序，简单选择排序 和直接插入排序法。在这一篇中，我们介绍4种改进的排序算法：希尔排序，堆排序，归并排序，快速排序。

I. 希尔排序

希尔排序。又叫缩小增量排序算法，是一个效率提升版的插入排序算法。也是冲破$O(n^2)$ 算法复杂度的第一批算法。与插入排序的不同的是，它会跳着比较元素间的大小。

所谓的跳着比较，就是 希尔算法 会定义一个 gap 值，例如 gap = array.length / 2， 就是将 n 个元素的数组分为了 n/2 组，包括 {0,n/2},{1,1+n/2} …{n/2-1,n-1} (这里的数字表示在数组中的位号)，每一组当做一个单独数组进行插入排序。完成后，再调整 gap = gap/2, 重复上述步骤，直到 gap 变为 1。具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static int[] shell_sort(int[] array) {
    int len = array.length;
    int temp, gap = len / 2;    //gap 序列
    while (gap > 0) {
        for (int i = gap; i < len; i++) {
            temp = array[i];
            int index = i - gap;        //以 gap 为间距的序列
            while (index >= 0 && array[index] > temp) {
                array[index + gap] = array[index];
                index -= gap;
            }
            array[index + gap] = temp;
        }
        gap /= 2;
    }
    return array;
}

需要注意的是，对于 shell sort 法，gap 的选取非常关键。整体来说，shell sort 法的时间复杂度为 $O(nlogn)$，高于之前介绍的3种算法。

II. 堆排序

对于上一节的选择排序，我们发现，每一次循环的比较，实际上只是为了一个元素的位置调整，而中间进行了很多次的比较，我们设想，如果可以在比较之后，将比较的结果通过某种方式进行一定形式的保存，从而减少后面重复的比较，最终减少比较的次数。

堆排序(Heap sort) 就是根据这一思想设计的排序方法。首先，它规定了一种数据结构：heap，它是具有下列性质的完全二叉树：

每个结点的值都大于或等于它的左右孩子的结点值，称为大顶堆 (或者每个结点的值都小于或等于它的左右孩子结点的值，称为小顶堆)。

将上面的描述用公式表述，即：$k_i \geq k_{2i}, k_i \geq k_{2i+1}$ 或者, $k_i \leq k_{2i}, k_i \leq k_{2i+1}$。这里的下标编号是从根结点开始层序遍历结点的编号值。

有了上述的分析，其实我们发现可以根据列表中的下标标号，对应数组中元素在完全二叉树中的位置。

对于堆排序算法，思路是这样的，首先构建一个最大堆，然后将堆顶元素放到最后一位，将完全二叉树的长度减1，重新调整剩下的元素为一个最大堆，再重复上述的步骤，直到堆中剩余1个元素位置。具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
//声明全局变量，用于记录数组array的长度；
static int len;

public static void swap(int[] array, int i, int j){
    int temp = array[i];
    array[i] = array[j];
    array[j] = temp; 
}

public static int[] heap_sort(int[] array) {
    len = array.length;
    if (len < 1) return array;
    //1.构建一个最大堆
    buildMaxHeap(array);
    //2.循环将堆首位（最大值）与末位交换，然后在重新调整最大堆
    while (len > 0) {
        swap(array, 0, len - 1);
        len--;
        adjustHeap(array, 0);
    }
    return array;
}

public static void buildMaxHeap(int[] array) {
    //从最后一个非叶子节点开始向上构造最大堆
    for (int i = (len/2 - 1); i >= 0; i--) {  
        adjustHeap(array, i);
    }
}

public static void adjustHeap(int[] array, int i) {
    int maxIndex = i;
    //如果有左子树，且左子树大于父节点，则将最大指针指向左子树
    if (i * 2 < len && array[i * 2] > array[maxIndex])
        maxIndex = i * 2;
    //如果有右子树，且右子树大于父节点，则将最大指针指向右子树
    if (i * 2 + 1 < len && array[i * 2 + 1] > array[maxIndex])
        maxIndex = i * 2 + 1;
    //如果父节点不是最大值，则将父节点与最大值交换，并且递归调整与父节点交换的位置。
    if (maxIndex != i) {
        swap(array, maxIndex, i);
        adjustHeap(array, maxIndex);
    }
}

构建过程中，我们只分析了 n/2 个非终端结点，因此, 时间复杂度仅为 $O(n)$。后续的移动堆顶操作，每一次调整的时间复杂度 为 $O(logi)$, （因为二叉树的某个结点i到根结点的距离为 $\lfloor log_2i \rfloor + 1$）,这样的操作需要执行 $n-1$ 次。因此，重建堆的时间复杂度为 $O(nlogn)$，从而整体堆排序的时间复杂度为 $O(nlogn)$.

堆排序对原始记录状态不敏感，即最好，最坏及平均情况，时间复杂度均为 $O(nlogn)$。但由于初始构建堆比较次数较多，对于排序序列个数很少的情况，不推荐使用。

III. 归并排序

归并排序（Merging Sort）将初始含有 n 个元素的序列看成是 n 个有序的子序列，每个子序列的长度为1，然后两两归并，得到 $\lceil n/2 \rceil$ 个长度为 2 或 1 的有序子序列；再两两归并，…，如此重复直到得到一个长度为 n 的有序序列为止。这种算法称为 两路归并排序。

归并算法实际上是基于的“分而治之”的思想，(divide and conquer), 代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public static int[] merge_sort(int[] array) {
    if (array.length < 2) return array;
    int mid = array.length / 2;
    int[] left = Arrays.copyOfRange(array, 0, mid);
    int[] right = Arrays.copyOfRange(array, mid, array.length);
    return merge(merge_sort(left), merge_sort(right));
}
/**
    * 归并排序——将两段排序好的数组结合成一个排序数组
    */
public static int[] merge(int[] left, int[] right) {
    int[] result = new int[left.length + right.length];
    for (int index = 0, i = 0, j = 0; index < result.length; index++) {
        if (i >= left.length)
            result[index] = right[j++];
        else if (j >= right.length)
            result[index] = left[i++];
        else if (left[i] > right[j])
            result[index] = right[j++];
        else
            result[index] = left[i++];
    }
    return result;
}

归并算法的时间复杂度为 $O(nlogn)$，但空间复杂度很高，为$O(n+logn)$。因此，归并算法是一个比较占用内存，但效率较高且稳定的一种算法。

对于内存占用的问题，可以使用非递归式的归并算法，空间复杂度可以降低为 $O(n)$，并且避免使用递归，可以提升一定的时间性能。所以，更加推荐使用非递归式的归并算法。

IV. 快速排序

快速排序是非常有名的算法，它最早由图灵奖获得者 Tony Hoare 提出，被列为20世纪十大算法之一。

快速排序（quick sort）的基本思想是：通过一趟排序将待排记录分割成独立的两部分，其中一部分的记录的关键字 均比 另一部分记录的关键字小，则可分别对这两部分记录进行排序，以达到整个序列有序的目的。

具体实现时，我们需要设置一个 pivot（枢轴）值，然后通过 partition 操作，将小于 pivot 的值放在序列的最左边，大于它的值放在序列的右边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
    * 快速排序方法
    */
public static int[] quick_sort(int[] array, int start, int end) {
    if (array.length < 1 || start < 0 || end >= array.length || start > end) return null;
    int smallIndex = partition(array, start, end);
    if (smallIndex > start)
        quick_sort(array, start, smallIndex - 1);
    if (smallIndex < end)
        quick_sort(array, smallIndex + 1, end);
    return array;
}
/**
    * 快速排序算法——partition
    */
public static int partition(int[] array, int start, int end) {
    int pivot = (int) (start + Math.random() * (end - start + 1));  
    // pivot 是随机选择的一个数字
    int smallIndex = start - 1;
    swap(array, pivot, end);
    for (int i = start; i <= end; i++)
        if (array[i] <= array[end]) {   
            //将比 array[end]小的值都放在队列的最前面
            smallIndex++;
            if (i > smallIndex)
                swap(array, i, smallIndex);
        }
    return smallIndex;      
    //smallIndex 前面的值都是比pivot值小的，so再以 smallIndex 为分界点，分两组排序
}

可以看出，快速排序法也是基于分治的思想，因而，它的时间复杂度与对应的分组二叉树的深度有关。在最有的情况，分组的二叉树相对平衡，需要执行的循环次数为 $log_2n$，每次循环需要比较 n 次，因此总的算法的时间复杂度为 $O(nlogn)$。而在最坏的情况下，分组不合理，时间复杂度可能为 $O(n^2)$。平均情况下，它的时间复杂度为 $O(nlogn)$。

空间角度来说，递归造成的栈空间的使用开销较大，平均的空间复杂度为 $O(logn)$。

但是，由于关键字的比较和交换是跳跃进行的，因此，快速排序算法是一种不稳定的排序算法。

针对上述的问题，我们可以从四个角度对传统的快速排序算法进行优化：

  1. 枢轴的选取问题：在书中，最传统的方法是总是选取一个固定位置的值作为枢轴的值，然而，这样的选取对一些有一定顺序的序列来说，可能会严重影响排序的效率。例如：对于一个倒序排列的序列，如果我们总是选取序列的首元素作为枢轴元素，那么最后对应的分组二叉树会极不平均。改进的方法包括 随机选取法 （上面示例代码中使用的方法）；三数取中法（先取三个关键字进行排序，然后选取中间大小的那一个）。
  2. 优化不必要的交换；（上面的示例代码做了这方面的考虑）
  3. 优化小数组时的排序方案。由于快速排序使用了递归的方法，因此对于一些数据量比较小的任何，它的效率反而不如简单的 直接插入算法， 因此，常用的操作是对待排序序列的长度进行判断，例如当 end - start < 7 的时候（也有推荐 50 作为分界的），我们就使用 简单插入算法，从而让两种算法优势互补，提升整体效率。
  4. 优化递归操作。书中对递归函数实施了 尾递归 优化，尽量减少系统的递归次数，可以提升效率。

V. 总结

根据以上的分析，我们可以将全部介绍的排序算法分为4大类：

  1. 插入排序算法:
    1. 直接插入排序；
    2. 希尔排序；
  2. 选择排序：
    1. 简单选择排序；
    2. 堆排序；
  3. 交换排序：
    1. 冒泡排序；
    2. 快速排序。
  4. 归并排序。

每个分类的子类中，上面的一个为简单算法，第二个为改进算法。

此外，我们还从时间复杂度（最好，平均，最坏情况），需要的辅助空间情况，算法的稳定性三个角度进行了分析。结果总结如下：

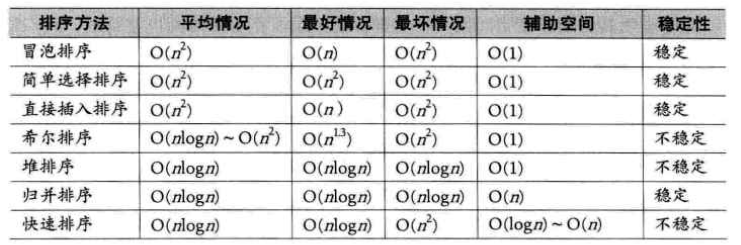
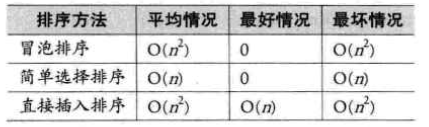
需要注意的是，在比较3种简单算法时，我们提到比较算法的时间复杂度实际上包括两个方面，即 “比较” 和 “移动” 两种操作的运算开销。从这个角度讲，如果整个记录的关键字信息量比较大，我们就更加推崇移动较少的算法。简单选择排序算法虽然在其他角度性能看似最差，但由于它的移动次数较少(三种简单算法的移动次数比较如下)，对于数据记录量不大而关键字信息量大的对象，简单排序具有优势。

部分代码参考: 郭耀华’s Blog. thx~