大话数据结构11-查找1

发表于 更新于 分类于 ， Valine：

搜索是互联网时代非常重要的一个技术。作者举了搜索引擎的例子，正是通过搜索引擎，使得人们能够更好的利用存储在互联网上的海量的数据。为了更好的抽象搜索的概念，我们引入以下几个定义：

  • 查找表（search table）：是由同一类型的数据元素（或者记录）构成的集合。
  • 关键字（Key）：是数据元素中某个数据项的值，又称为 键值。若此关键字可以唯一的标识一个记录，则称此关键字为 主关键字（Primary Key）；相对的，对于那些可以识别多个数据元素（或记录）的关键字，我们称之为 次关键字（Secondary Key）。

查找的过程，实际上就是根据给定的某个值，在查找表中确定一个（或多个）其关键字等于给定值的数据元素（或记录）。

I 顺序表查找

顺序查找（Sequential Search,也叫线性查找）是最为基本的查找方式，可以使用如下的循环结构进行。

1
2
3
4
5
6
7
8
//n 是数组 a 的长度，key 为要寻找的关键字
int Sequential_Search(int *a, int n, int key){
    for(i = 0;i <= n;i++){      
        if (a[i] == key)
            return i;
    }
return 0;
}

上述的代码实际上可以进一步优化，因为在循环过程中，我们每一步都需要将 i 与 n 进行比较，而实际上循环还会在一个条件下结束，就是 a[i] == key，那么，能否使用这个条件作为循环条件呢？因此有如下代码：

1
2
3
4
5
6
7
8
9
10
//有哨兵的顺序查找
int Sequential_Search2(int *a, int n, int key){
    a[0] = key; //设置a[0] 的值，我们称之为“哨兵”
    int i = n;
    while(a[i] != key){
        i--;
    }
        
    return i;   //如果return 为 0，说明查找失败
}

如上所示，我们通过将 a[0] 设置为 key, 添加一个“哨兵”，成功将循环的两个结束条件进行了统一，从而减少了每次循环所需要的执行的任务量，提升了代码的效率。

总的来说，无论上面哪种方式，顺序查找的时间复杂度都为 $O(n)$。

Note：上面的例子中，key 都为 主关键字。

II 有序表查找

线性表查找的效率较低，为了提升查找效率，我们进一步介绍有序表查找的方法。有序表查找是基于线性表有序的情况，即在存储时，数据是按照顺序进行排放的。

a. 折半查找法

折半查找（Binary Search）技术，又称为 二分查找。折半查找在有序表中取中间记录作为比较对象，若给定值与中间记录的关键字相等，则查找成功；若给定值小于中间记录的关键字，则在中间记录的左半区继续查找，同理，如果大于，则在中间记录的右半区继续查找。不断重复上述步骤直到找到对应元素(或查到查找区域无记录为止)。

实际上上述查找类似二叉树，查找的次数一定小于对应二叉树的深度，我们知道完全二叉树的深度为 $[log_2n]+1$ ([] 表示向下取整)，因此折半查找的时间复杂度为 $O(logn)$。

b. 插值查找

折半查找总是从最中间开始进行分块，然后判断，那么我们可否根据所要查找的元素的键值，动态的选取一个更加合适的分位点呢？

插值查找（Interpolation Search）基于这一思路，更新上述 折半查找 的分位点为：

$$mid’ = low + \frac{key-a[low]}{a[high]-a[low]}(high - low)$$

这里，a[] 为我们需要进行查找的数组，其中，key 是要查找的元素的关键字，a[low] 为该数组中的最小键值，a[high] 为最大键值。

c. 斐波那契查找

同样的，斐波那契查找（Fibonacci Search），也提供了一种计算中间分位值的方法：通过斐波那契数列获得（黄金分割）。

我们知道斐波那契数列为：

$$F = [0,1,1,2,3,5,8,13,21,34…]$$

我们首先根据数组 a[] 的元素个数 n，寻找到刚好大于 n 的斐波那契数列中的元素，例如 n = 20, 则对应斐波那契数列中的数 21 (i.e. F[8]), 找到该数之后，我们将原数组补齐到 21 个，然后设置分位点，mid = low + F[k-1] -1。

虽然 Fibonacci Search 的时间复杂度也为 $O(logn)$, 但对于数组中大大部分元素（除去key 值非常小的情况），Fibonacci Search 查找的效率会更高。

III 线性索引查找

上述的方法都是基于按顺序排列的数据，但如果数据量非常大，将所有数据进行排序显然不现实。因此，我们引入 - 索引，来提高数据的处理速度。

索引，就是把一个关键字与它对应的记录相关联的过程，一个索引由若干个索引项构成。每个索引项至少应包含 关键字 和 其对应的记录在存储器中的位置 等信息。

索引按照结构可以分为线性索引、树形索引和多级索引。所谓线性索引是将索引项集合组织成线性结构，也称为索引表。这里，介绍3种索引：稠密索引，分块索引和倒排索引。

a. 稠密索引

稠密索引是指在线性索引中，将数据集中每个记录对应一个索引项。并且，索引项按照关键码有序排列，如下图所示。Figure link

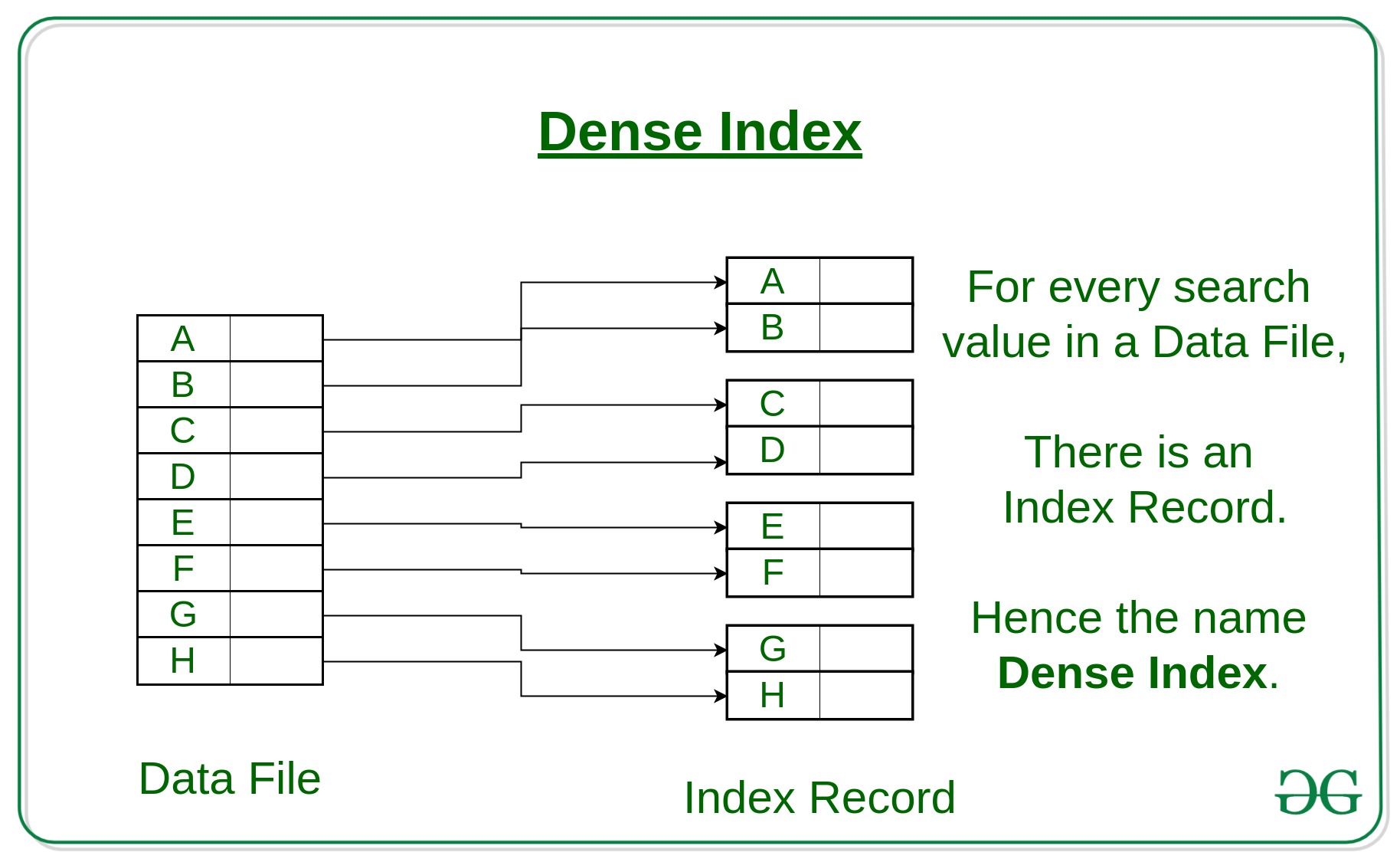
使用稠密索引法，搜索数据时，可以利用有序表查找首先找到对应的索引项，然后直接抵达目标结果。缺点是是当数据量非常大时，索引数据量也会非常大。

b. 分块索引

为了减少索引的个数，我们可以对数据集进行分块，使其分块有序，然后再对每一块建立索引项，从而减少索引项的个数。

所谓分块有序，是将数据集分成若干块，这些块需要满足:块内无序 and 块间有序(例如第二块的记录的关键字都大于第一块记录的关键字)。

我们假设 n 个记录的数据集，被平均分成了 m 块，每块中有 t 条记录 （t= n/m）。假设 $L_b$ 为查找索引表的平均查找长度，根据最好与最差等概率原则，$L_b$ 的平均长度为 $\frac{m+1}{2}$。$L_w$ 为块中查找记录的平均查找长度，同理可知它的平均查找长度为 $\frac{t+1}{2}$。

因此，分块索引查找的平均长度为：$ASL_w = L_b+L_w=\frac{1}{2}(m+t)+1=\frac{1}{2}(\frac{n}{t}+t)+1$. 当 m = t 时，结果最佳，此时：$ASL_w = \sqrt{n}+1$。

可见，分块索引法的查找效率比顺序查找 $O(n)$ 高，但是低于稠密存储可使用的 折半查找 $O(logn)$。因此，它是一种兼顾存储空间和算法复杂度的一种索引方法。

c. 倒排索引

在倒排索引法中，索引项包括：次关键码 + 记录号表。其中记录号表存储具有相同次关键字的所有记录号，这样的索引方法称为倒排索引法（inverterd inex）。之所以叫 “倒排”，是因为它使用的是次索引码，即不是唯一确定数据的主关键字，也因此记录号通常不唯一，可能有多个。所以，它相当于是根据属性反查记录位置的方法，因为称作倒排索引法。

IV 二叉排序树

二叉排序树查找算法 是一种 查找 以及 插入/删除效率 都很高的查找算法。

二叉排序树查找算法，需要将数据按特定顺序放在二叉树中，这种二叉树称为 二叉排序树(Binary Sort Tree), 又称二叉查找树。它具有如下性质：

  • 若它的左子树不为空，则左子树上所有的结点的值均小于它的根结点的值；
  • 若它的右子树不为空，则右子树上所有的结点的值均大于它的根结点的值；
  • 它的左右子树也分别为二叉排序树。

因此，上述二叉树的中序遍历的结果就是一个从小到大排列的序列。

二叉排序树以链式方式存储，因而具有链式存储结构在插入删除操作的高效率的优点。此外，由于数据在二叉树中按特定顺序存储，查找元素时从根结点，最多的次数最多为二叉排序树的层数。但是，由于根结点不确定，二叉排序树的形状因不同根结点的选取差别也很大，如下图所示（Figure link）：

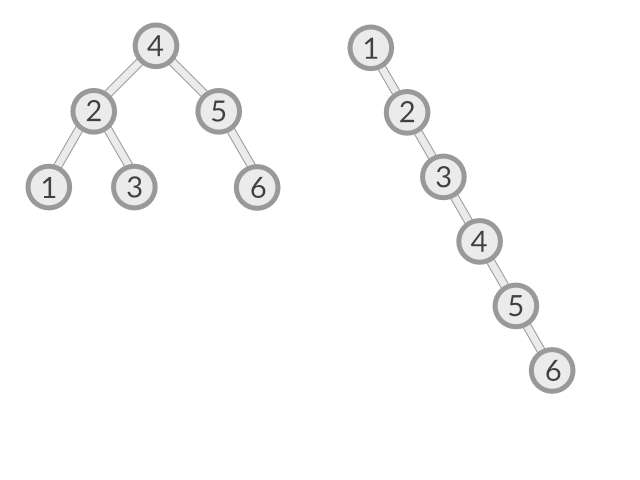
对于上图的左图，查找的时间复杂度约为 $O(logn)$,而对右图中的斜树而言，查找元素的时间复杂度与顺序查找相同，为 $O(n)$。因此，我们希望二叉排序树尽量平衡，以获得更高的查找效率。