大话数据结构10-图2

发表于 更新于 分类于 ， Valine：

上节中，我们介绍了图的基本概念以及他的基本操作：存储、遍历方法。这一节，我们更加深入的探讨一些图的相关的实际应用，包括：最小生成树，最短路径 和 有向无环图 的拓扑排序和关键路径问题。每一个应用下，都介绍了几种算法，在这一过程中，我们可以更加深入的了解图的结构及它的相关操作。

I 最小生成树

我们把构造连通网的最小代价生成树称为最小生成树（Minimum cost spanning tree）。寻找连通网的最小生成树，经典的有两种算法，普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法。

a. Prim 算法

假设 $N = (P,\{E\})$ 是连通网，$TE$ 是 $N$ 上最小生成树中边的集合。算法从 $U=\{u_0\}(u_0\in V)$, $TE=\{\}$ 开始，重复执行下述操作：在所有 $u\in U, v\in (V-U)$ 的边 $(u,v)\in E$ 中找到一条代价最小的边 $(u_0,v_0)$ 并入集合 $TE$, 同时$v_0$ 并入 $U$, 直到 $U=V$ 为止。此时，$TE$ 中必有 $n-1$ 条边，则 $T=(V,\{TE\})$ 为 $N$ 的最小生成树。

通俗一点讲，就是将上述 $U$ 看做一个广义的”点”，然后寻找到这个点距离最短的一个具体顶点，并入 $U$， 再重复以上运算的过程。

对于n个顶点的图，Prim 算法的时间复杂度为 $O(n^2)$.(具体参见代码)

b. Kruskal 算法

不同于 Prim 算法找点的方式，Kruskal 算法基于的是直接去找edge。在上一篇图的存储章节中我们介绍了边集数组的存储方法，Kruskal 算法就基于这个数组实现，所做的首先是将该数组按照权值排序。

具体的，假设 $N=(V,\{E\})$ 是连通网，则令最小生成树的初始状态为只有 $n$ 个顶点而无边的非连通图 $T=(V,\{\})$, 图中每个顶点自成一个连通分量。在 $E$ 中选择代价最小的边，若该边依附的顶点落在 $T$ 中不同的连通分量上，则将此边加入到 $T$ 中，否则舍去此边而选择下一条代价最小的边。依次类推，直至 $T$ 中所有顶点都在同一连通分量上为止。

对于有 $e$ 条边的图，Kruskal 算法的时间复杂度为 $O(elog(e))$。

II 最短路径

对于网图来说，最短路径是指两顶点之间经过的边上权值之和最少的路径，并且我们称路径上的第一个顶点是 源点，最后一个顶点是 终点。为求最短路径，我们在这里介绍两种算法。

a. Dijkstra（迪杰斯特拉）算法

Dijkstra 算法不是直接一步到位去求两点间的最短路径，而是选取两点中的一点为起点，一步一步求得与它最接近的点的最短距离，与之稍远的点之间的最短距离，与之相距更远的点之间的最短距离，直到达到最终结果。

实际上，Dijkstra 算法求得了源点到其余各定点之间的最短路径，并且算法的时间复杂度为 $O(n^2)$。

此外，如果我们需要直到所有点到所有点的最短路径，我们可以使用 Dijkstra 算法对 n 个点再进行一次循环，从而时间复杂度变为 $O(n^3)$。

b. Floyd 算法

类似的， Floyd 算法同样可以在 $O(n^3)$ 的时间复杂度下求得所有点到所有点的最短距离，并且实现更加优雅。

具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
typedef int Pathmatrix [MAXVEX][MAXVEX];
typedef int ShortPathTable [MAXVEX][MAXVEX];
// Floyd 算法，求网图 G 中各顶点 v 到其余顶点 w 最短路径 P[v][w]及带权长度 D[v][w] 
void ShortestPath_Floyd(MGraph G, Pathmatrix *P, ShortPathTable *D){
    int v,w,k;
    for(v = 0;v<G.numVertexes; ++v){
        for(w = 0; w<G.numVertexes;++w){
            (*D)[v][w] = G.matrix[v][w];    //D[v][w] 值即为对应点间的权
            (*P)[v][w] = w;                 //初始化 p
        }
    }
    for(k = 0;k<G.numVertexes; ++k){
        for(v = 0;v<G.numVertexes; ++v){
            for(w = 0;w<G.numVertexes; ++w){
                if((*D)[v][w]>(*D)[v][k] + (*D)[k][w]){
                    //如果经过下标为 k 顶点路径比原两点间路径更短
                    //则将当前两点间的权值设为更小的一个
                    (*D)[v][w] = (*D)[k][k] + (*D)[k][w];
                    (*P)[v][w] = (*P)[v][k];    //路径设置经过下标为k的顶点
                }
            }
        }
    }
}

III 拓扑排序-针对AOV网

在一个表示工程的 有向图 中，用顶点表示活动，弧表示活动之间的优先关系，这样的有向图为顶点表示活动的网，我们称为 AOV 网。（activity on vertex network）。与树结构不同的是，可能有多个弧指向同一个顶点，而树的每一个结点只能有一个父节点。

设 $G = (V,E)$ 是一个具有 n 个顶点的 有向图，$V$ 中的顶点序列 $v_1,v_2, … v_n$，若满足从顶点 $v_i$ 到 $v_j$ 有一条路径，则在顶点序列中 $v_i$ 必定在 $v_j$ 之前。则我们称这样的顶点序列为一个 拓扑序列。

对一个有向图构造拓扑序列的过程称为 拓扑排序。如果得到的拓扑序列输出了此网的全部顶点，则说明它是不存在环（回路）的 AOV 网；如果输出顶点数少于总顶点数，则说明这个网存在环（回路），不是 AOV 网。

针对 AOV 网进行拓扑排序的基本思路如下：从 AOV 网中选择一个入度为 0 的顶点输出，然后删去此顶点，并删除此顶点为尾的弧，并继续重复此步骤，直到输出全部顶点或者 AOV 网中不存在入度为 0 的顶点为止。根据上述描述，拓扑排序的过程涉及顶点的删除，显然使用邻接表会更加方便。

IV 关键路径-针对AOE网

在一个表示工程的 带权有向图 中，用顶点表示事件，有向边表示活动，用边上的权值表示活动的持续时间，这种有向图的边表示活动的网，我们称之为 AOE 网（Activity On Edge Network）。我们将 AOE 网 中没有入边的顶点称为 始点 或 源点，没有出边的顶点称为 终点 或 汇点。

一个简单的 AOV 和 AOE 的例子如下。可见， 虽然两者都是对于工程的建模，但是 AOV 网只描述活动之间的制约关系，而 AOE 网则在 先后顺序信息 的基础上，增加了权值信息。

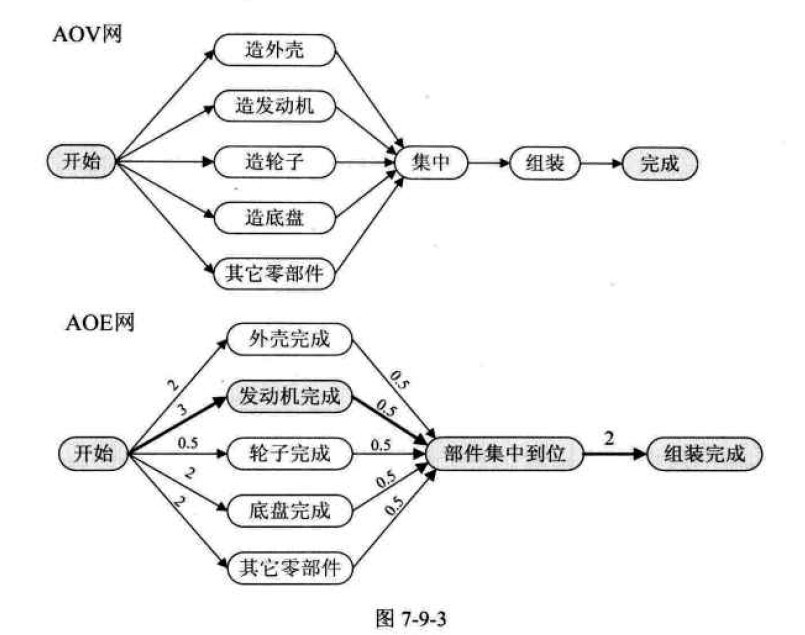
对于 AOE 网来说，满足如下两点：

  1. 只有某顶点的事件发生后，从该顶点出发的各项活动才能开始；
  2. 只有进入某顶点的各项活动都已经结束，该顶点的事件才能发生。

我们把路径上各个活动所持续的时间之和称为 路径长度，从源点到汇点具有最大长度的路径叫做 关键路径，在关键路径上的活动叫做 关键活动。时间上，关键路径是完成整个工程所需要的最短的时间，之所以称之 关键，是因为若想要提升整个工程的效率，必须从关键路径的关键活动入手，减少时间，从而缩短整个工期。

寻找关键路径的算法的核心是寻找到一个个的关键活动，为寻找关键活动，我们首先做如下的几个定义：

  1. 事件 的最早发生时间 etv (earliest time of vertex)：即顶点 $v_k$ 的最早发生时间；
  2. 事件 的最晚发生时间 ltv (latest time of vertex): 即顶点 $v_k$ 的最晚发生时间，也就是每个顶点对应事件最晚需要开始的时间，超过该时间将会延误整个工期；
  3. 活动 的最早开工时间 ete (earliest time of edge): 即弧 $a_k$ 的最早发生时间；
  4. 活动 的最晚开工时间 lte (latest time of edge):即弧 $a_k$ 的最晚发生时间，也就是不推迟工期的最晚开工时间。

寻找 关键活动时，我们首先由 1,2 中的“事件”时间 求得 3,4 中的“活动”时间，然后再根据 ete[k] 是否与 lte[k] 相等来判断 $a_k$ 是否是关键活动。

类似于处理 AOV网 的拓扑排序问题，我们也使用邻接表结构存储图，来处理 AOE 的关键路径问题，具体代码此处略。

V 图总结

图的存储结构中，比较基础和重要的是 邻接矩阵 和 邻接表，他们分别是将 边集 存储在数组中 和 链表中。十字链表 是 对邻接表的一种升级，而 邻接多重表 和 边集数组 则更多的考虑的是对边的关注。存储结构的选择与所处理的数据特征及需要进行的操作有关，例如对于稠密图，或者读存数据较多，结构修改较少的图，使用 邻接矩阵 更加合适，反之，则更加推荐 邻接表存储。

此外，我们还介绍了图的三种应用：最小生成树，最短路径和有向无环图（AOE，AOV）的应用。

最小生成树的两种算法，prim 算法是走一步看一步的思维方式，逐步生成最小生成树。而 Kruskal 算法则更有全局意识，直接从权值最小的边入手，寻找答案。

最短路径的实现方法很多，Dijkstra 算法从单个顶点开始逐步查找最短路径，符合我们的正常思维。而 Floyd 算法则抛开了单点局限思维，应用矩阵的变换，用简洁的代码实现了最短路径的求解，但原理理解相对较难。