大话数据结构9-图1
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成的,通常表示为 $G(V,E)$, 其中,$G$ 表示一个图,$V$ 是图 $G$ 中顶点的集合,$E$ 是图 $G$ 中边的集合。
图中的数据元素称为 顶点(Vertex),不同于线性表和树允许有空表、空树,图中不允许没有顶点。在图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用 边(edge) 来表示,所有的边的集合为 边集,且边集可以为空。
I 图的相关定义
有向图和无向图
对于两个顶点间没有规定方向的边我们称为 无向边(edge),用 无序偶对$(v_i,v_j)$ 表示。对于所有边都是无向边的图,我们称之为 无向图(undirected graphs)。
对于顶点间有方向定义的边我们称为 有向边,也称为 弧(Arc)。用有序偶$\langle v_i,v_j \rangle$ 表示(由 $v_i$ 到 $v_j$ 的弧),其中 $v_i$ 称为 弧尾(Tail),$v_j$ 称为 弧头(head)。如果图中任意两个顶点之间的边都是有向边,该图为 有向图。
完全图
在无向图中,如果任意两个顶点之间都存在边,则称该图为 无向完全图。含有 n 个顶点的无向完全图中有 $\frac{n\times(n-1)}{2}$ 条边。
而在有向图中,如果任意两个顶点之间都存在方向相反的两条弧,则称该图为 有向完全图。n 个顶点的有向完全图共有 $n(n-1)$ 条边。
图的度
对于无向图 $G=(V,{E})$, 如果 边$(v,v’)\in E$, 则称顶点 $v$ 和 $v’$ 互为 邻接点(adjacent),即$v$与 $v’$ 相邻接。边$(v,v’)$ 依附(incident)于顶点 $v$ 和 $v’$, 或者说 $(v,v’)$ 与顶点 $v$ 和 $v’$ 相关联。顶点 $v$ 的 度(degree) 是和 $v$ 相关联的边的数目,记为 $TD(v)$。
对于有向图 $G=(V,{E})$, 如果 弧$\langle v,v’\rangle \in E$, 则称顶点 $v$ 邻接到顶点 $v’$,或称 顶点 $v’$ 邻接自顶点 $v$。弧 $\langle v,v’\rangle$ 与顶点 $v$ 和 $v’$ 相关联。以顶点 $v$ 为头的弧的数目 称为 $v$ 的 入度(InDegree),记为 $ID(v)$;以 $v$ 为尾的弧的数目称为 $v$ 的 出度(OutDegree),记为 $OD(v)$。顶点 v 的 度 为 $TD(v) = ID(v)+OD(v)$。
路径
无向图 $G=(V,{E})$中从顶点 $v$ 到顶点 $v’$ 的 路径(path) 是一个顶点序列 $(v = v_{i,0},v_{i,1},…,v_{i,m}=v’)$, 其中 $(v_{i,j-1},v_{i,j})\in E$. (对于有向图,定义类似) 路径的长度是路径上 边或弧的数目。
在图中,若不存在顶点到其自身的边,且同一条边不重复出现,则称这样的图为 简单图。
第一个顶点和最后一个顶点相同的路径称为 回路或环(cycle),序列中顶点不重复出现的路径称为 简单路径。除了第一个和最后一个顶点外,其余顶点不重复的回路称为 简单回路 或 简单环。
连通图
在无向图 $G$ 中,如果从顶点 $v$ 到 顶点 $v’$ 有路径,则称 $v$ 和 $v’$ 是连通的。如果对于图中任意两个顶点 $v_i, v_j\in V$, $v_i$ 和 $v_j$ 都是连通的,则称 $G$ 是 连通图(Connected Graph)。无向图中的 极大连通子图 称为 连通分量(Connected Component)。
在有向图 $G$ 中,如果对于每一对 $v_i, v_j\in V, v_i \neq v_j$, 从 $v_i$ 到 $v_j$ 和从 $v_j$ 到 $v_i$ 都有路径,则称 $G$ 是 强连通图。有向图中的 极大强连通子图 称做有向图的 强连通分量(strongly connected components)。如下图中所示,图中有3个 强连通分量。
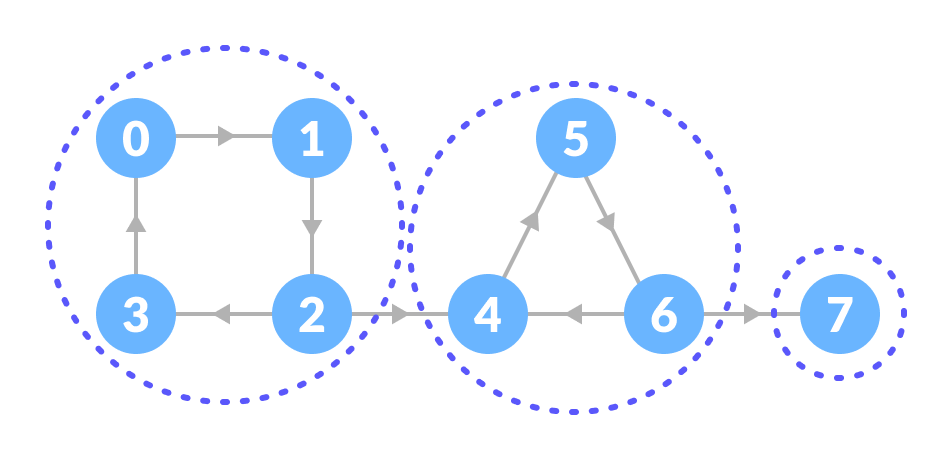
一个连通图的 生成树 是一个极小的连通子图,它含有图中全部的 $n$ 个顶点,但只有足以构成一棵树的 $n-1$ 条边。(Note: 如果一个无向图 $G$ 有 $n$ 个顶点,如果边的数量小于 $n-1$,则一定是非连通图,如果边的数量多于 $n-1$,则必定可以构成一个环)
对于有向图,如果恰有一个顶点的入度为0,其余顶点的入度均为1,则是一棵 有向树。一个有向图的 生成森林 由若干棵有向树组成,含有图中全部顶点,但只有足以构成若干棵不相交的有向树的弧。
Others
与图的边或者弧相关的数字叫做 权(weight)。(例如两个点之间的距离)。这种带权的图通常称为 网(network)。
假设有两个图 $G=(V,{E})$ 和 $G’=(V’,{E’})$,如果 $V’\subseteq V$, 且 $E’\subseteq E$, 则称 $G’$ 为 $G$ 的子图(subgraph)。
II 图的存储结构
对于图来说,由于它不存在一个类似线性表的头尾,以及树的根结点之类的东西,利用利用传统的顺序存储方式很难存放。虽然链表可以表示图中 顶点 间的关系,但若图的顶点的 度 之间相差很大的话,会使得链表的结点难以设计。因此,对于图,我们使用一些更加特殊的结构来进行存储。
a. 邻接矩阵
考虑到图是由定点和边(或弧)两部分组成的,我们可以考虑将他们分开存储。顶点由于不分大小主次,所以可以用一个一维数组来存储。而边和弧 由于是顶点与顶点间的关系,我们考虑使用二维矩阵的方式存储。因此有了下面的 邻接矩阵(Adjacency Matrix) 存储方式。
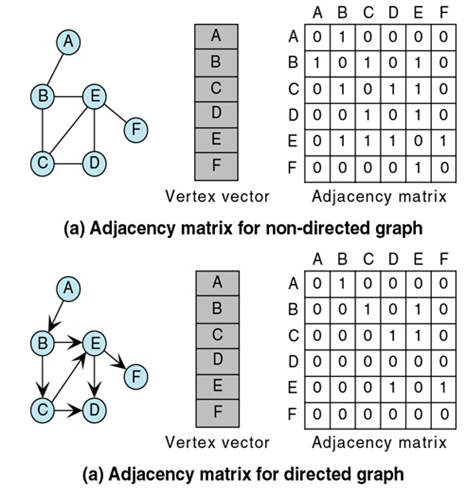
由上图可以发现,矩阵对应的位置为 $a_{ij}$ 为1,说明顶点 $i,j$ 之间有连线。对于无向图来说,它的边数组(矩阵)一定是一个对称矩阵,即 $a_{ij} = a_{ji}$.
此外,对于 网 的概念,也就是每条边上带有权的图,我们也可以将这些权值存储在adjacency matrix 中。如下所示:
$$
arc[i][j]=
\begin{cases}
w_{ij} & \quad 若 (v_i,v_j)\in E \ or\ \langle v_i,v_j\rangle \in E\\
0 & \quad i = j\\
\infty & \quad i,j 之间无连接\\
\end{cases}
$$
其中,$w_{ij}$ 为 $(v_i,v_j)$ 或者 $\langle v_i,v_j\rangle$ 的权值。这里使用 $\infty$ 表示两个点之间没有连接,是因为两点间连接的权值可能为0,因此使用一个不可能出现的权值作为两点间的数值。
由于矩阵是 $n*n$ 的形式,我们可知初始化这样的邻接矩阵的时间复杂度为 $O(n^2)$.
b. 邻接表
对于较为稀疏的图(边的数量相对顶点少很多),使用数组会造成很大的空间浪费,因此我们考虑结合数组和链表进行存储,称为 邻接表(adjacency list)存储。具体如下:
- 图中的顶点使用一个一维数组进行存储,并在数组中添加指向该顶点第一个邻接点的指针。
- 图中的每个顶点 $v_i$ 的所有邻接点构成一个线性表,使用单链表进行存储。无向图称为顶点 $v_i$ 的边表,有向图则称为顶点 $v_i$ 作为弧尾的出边表。
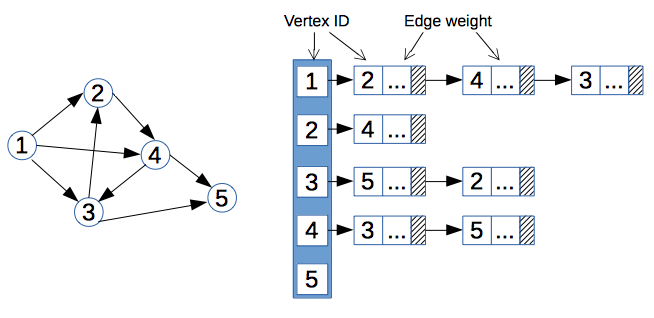
对于有向图,我们也可以对每个顶点 $v_i$ 建立一个链接为 $v_i$ 为弧头的表,称为 有向图的 逆邻接表。
通过邻接表,我们可以快速的计算 顶点的 度 or 出度、入度。
c. 十字链表
对于有向表,为了解决邻接表只能记录图的 出度 或 入度 的缺点,我们引入 十字链表(orthogonal List)。如下图所示,我们重新定义顶点表结构,使得其中同时存储 出弧 和 入弧 的顶点位置。同时,边表结构也重新定义如下,边表中前两个位置同时存储弧头和弧尾的信息,后两个位置则分别存储与前面弧头、弧尾同弧头,和同弧尾的顶点的位置。
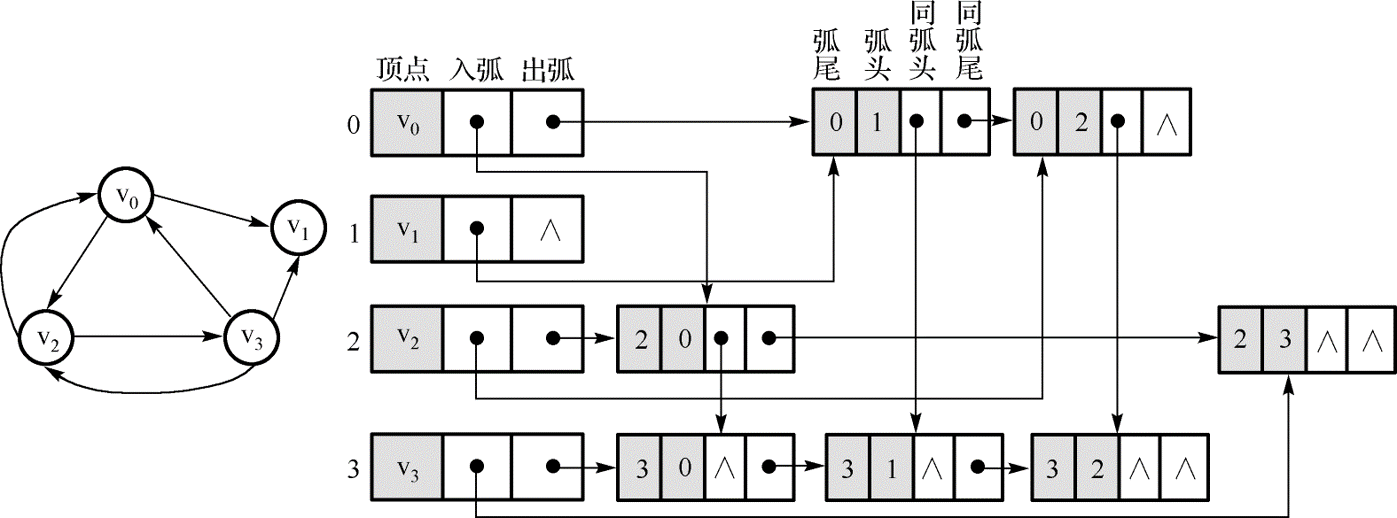
可见,十字链表将邻接表和逆邻接表整合在了一起,这样很容易可以求得顶点的出度和入度。此外,它除了结构稍复杂外,创建时的时间复杂度与邻接表是相同的,因此,在有向图的应用中,十字链表是比较推荐的数据结构模型。
d. 邻接多重表
邻接表结构关注的是图的顶点,以顶点为核心拉出一条一条的链表存储它的邻接顶点。但是如果我们更加关注边的操作,邻接表的存储方式就会相对繁琐。
因此我们设计邻接多重表结构,重点关注边的存储,以类似链表的形式将与顶点关联的边都联系起来。如下图中所示。
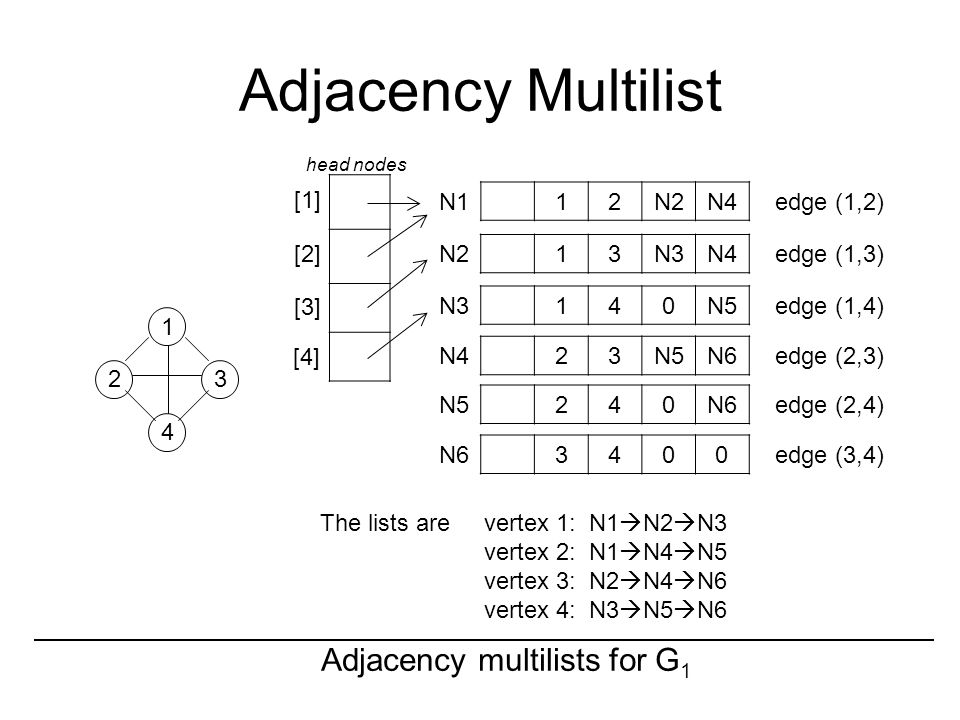
(上图与书中描述的邻接多重表相比,表中结点存储的内容相同,但顺序稍有不同。)上图的边表中,边表结点的第二,第三个位置,存储了相连接的两个顶点$v_i,v_j$,第四和第五个位置,则分别存储了一个与顶点 $v_i$ 和 $v_j$ 相连接的其他的边。可以看出,对于邻接多重表,存储关注的重点是边的存储,有多少条边就一共有多少个边结点。
e. 边集数组
类似上面的多重表,另一关注边的存储的图存储结构称为边集数组。它使用两个一维数组分别存储顶点信息和边信息。边信息数组每个数组元素由起点下标、终点下标和权组成。如下图所示。
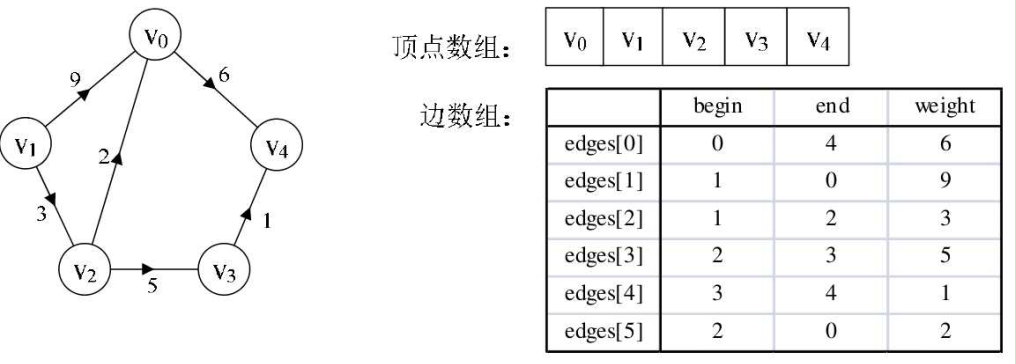
边集数组同样适合于对边进行操作的处理,而不适合对顶点的操作。(在后面的克鲁斯卡尔(Kruskal)算法中有详细应用介绍)
III 图的遍历
我们希望从图中的某一定点出发访遍图中其余顶点,且使每个顶点仅被访问一次,这一过程称为图的遍历(traversing graph)。
但与树等结构不同,图没有明确的层次结构,因此我们需要在遍历过程中把访问过的顶点打上标记以避免多次访问。通常办法是设置一个访问数组 $visited[n]$,n 是图中的顶点的个数,初值为0,访问过之后就是1。
对于图的遍历,根据希望侧重的方向,我们将之分为两种:深度优先的遍历算法和广度优先的遍历算法。
a. 深度优先的遍历算法
深度优先遍历(Depth First Search)也称为深度优先搜索,简称 DFS。具体的,深度优先算法从图中的某个顶点出发,访问次顶点,然后从 $v$ 的未被访问的邻接点出发深度优先遍历图,直到图中所有和 $v$ 有路径相通的顶点都被访问到。对于非连通图,只需要对它的连通分量分别进行深度优先的遍历即可。
直观一点讲,深度优先的遍历算法有点类似树的前序遍历算法,先清理完毕根结点的左子树结点,再回溯上去,依次清理未达的结点。
b. 广度优先遍历算法
广度优先遍历(Breadth First Search),又称为广度优先搜索,简称 BFS。具体的,有点类似树的层序遍历算法,首先选取一个起点,然后根据与该顶点的连接关系,分层遍历。
c. 对比分析
下图,我们可以形象的看出深度优先搜索算法与广度优先搜索算法的区别(虽然画的是树结构,但是原理一样):
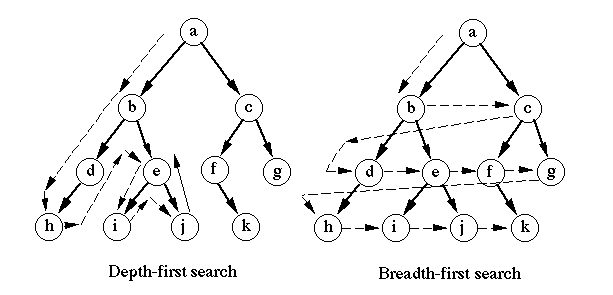
通常来说,这两种算法的时间复杂度是接近的,不同的仅是访问次序的差别。但是对于搜素特定目标顶点的任务,深度优先算法更加适合目标比较明确的情况,而广度优先算法则可以通过扩大遍历范围找到相对最优解的情况。