大话数据结构8-树2

发表于 更新于 分类于 ， Valine：

I 线索二叉树

线索二叉树的构想主要来源于两个问题，1- 二叉链表存储结构让每个结点都有左右指针，但部分结点无左子树/右子树/both。2- 二叉链表不存储结点的前驱、后继结点的信息（（Note：这里的前驱、后继是针对某种遍历方法而言的，前驱指遍历时该结点前一个结点，后继类似。）。

我们把指向前驱和后继的指针称为线索（thread），加上线索的二叉链表称为线索链表，相应的二叉树就称为线索二叉树（Threaded Binary Tree）。在线索二叉树中，为了知道地址域中存放的是前驱/后继 还是左右child，我们另外设置两个布尔型的标志域 ltag, rtag ，规定标志域为 0 时表示 左/ 右child。

如下图所示，中序遍历后，我们将所有空指针域的 rchild 指向它的后继结点，空指针域的 lchild 指向当前结点的前驱结点。

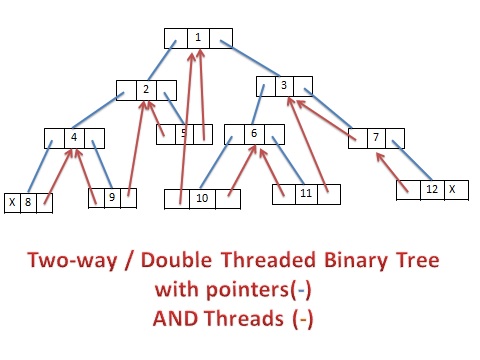
我们将对二叉树以某种遍历次序使其变为线索二叉树的过程称为线索化，线索化后的二叉树充分利用了存储空间，此外，也将一棵二叉树转变为了一个双向链表，从而更加有利于我们插入删除结点。

我们以中序遍历为例，线索化的递归函数代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
BiThrTree pre;  //全局变量，始终指向刚刚访问过的结点
//中序遍历进行中序线索化
void InThreading (BiThrTree p){
    if(p){
        InThreading(p->lchild);     //递归左子树线索化
        if(!p->lchild){         //没有左孩子
            p->LTag = Thread;   //前驱线索
            p->lchild = pre;    //左孩子指针指向前驱
        }
        if(!pre->rchild){           //前驱没有右孩子
            pre->RTag = Thread;     //后继线索
            pre-rchild = p;         //前驱右child指针指向后继
        }
        pre = p;                    //保持 pre 指向p 的前驱
        InThreading(p->rchild);     //递归右子树线索化
    }
}

通过上述代码可以发现，中序线索化的过程与之前中序遍历的代码几乎一样，只是将中间的执行代码换为了线索化功能。

有了线索二叉树之后，我们对它进行遍历时就等于操作一个双向链表。类似双向链表，我们给线索二叉树添加一个头结点，并令它的 lchild 域的指针指向二叉树的根结点，rchild 指向二叉树的最后一个结点，then 令二叉树中序遍历序列的第一个结点的 lchild 以及最后一个结点的 rchild 都指向头结点。这样做之后，我们既可以从第一个元素起顺后继遍历，也可以从最后一个元素起顺前驱进行遍历。具体遍历代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//T 指向头结点，头结点左链 lchild 指向根结点，
//头结点右链rchild指向中序遍历的最后一个结点
// T 为中序遍历二叉线索链表表示的二叉树
Status InOrderTraverse_Thr(BiThrTree T){
    BiThrTree p;
    p = T->lchild;      //p指向根结点
    while(p != T){      //空树或者遍历结束时， p == T
        while(p->LTag == Link)  //当LTag==0时循环到中序序列的第一个结点
            p = p->lchild;
        printf("%c",p->data);   //显示结点数据
        while(p->RTag == Thread && p->rchild != T){
            p = p->rchild;
            printf("%c",p->data);
        }
        p = p->rchild;      //p进至其右子树根
    }
    return OK;
}

II 树、森林与二叉树的转换

相对于一般的树，二叉树的结构更加标准化，因此存储读取都可以效率更高，因此我们希望将一般的树转换为二叉树，具体的方法如下：

  1. 加线，在所有相邻兄弟结点之间加一条连线。
  2. 去线，对树中每个结点，只保留它与第一个孩子结点的连线，删除它与其他孩子结点之间的连线。
  3. 层次调整，便于查看。注意第一个孩子是二叉树结点的左孩子，兄弟转换过来的孩子为右孩子。

此外，我们还可以设计一套标准的将森林转变为二叉树的过程：

  1. 把每一棵树转为二叉树；
  2. 第一棵二叉树不动，从第二棵开始，依次把后一棵树的根结点作为前一棵树根结点的右孩子。

III 赫夫曼树及其应用

我们规定，从树中一个结点到另一个结点之间的分支构成两个结点之间的 路径，路径上的分支数目称为 路径长度。而 树的路径长度，就是从树根到 每个结点(不仅仅是叶结点) 的路径长度之和。

此外，如果考虑带权的结点，结点的 带权路径长度 为从该结点到树根之间的路径长度乘上该节点的权。树的带权路径长度 为树中所有 叶结点 的带权路径长度之和。其中，带权路径长度（WPL）最小的二叉树称为 赫夫曼树，也叫 最优二叉树。（WPL 定义解释如下）

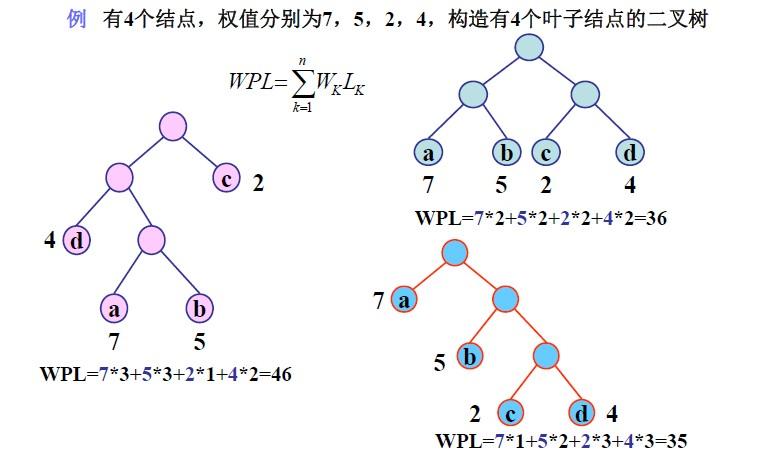
那么如何产生赫夫曼树呢，我们给出如下步骤：

  1. 根据给定的 n 个权值 ${w_1,w_2,..w_n}$ 构成 $n$ 棵二叉树的集合 $F = {T_1,T_2,…T_n}$, 其中每棵树中只有一个带权为 $w_i$ 的根结点，其左右子树为空。
  2. 在 $F$ 中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，该新树的根结点的权值为其左右子树根结点权值之和。
  3. 在 $F$ 中删除2中的两棵子树加入他们生成的新子树。
  4. 重复2，3步，直到 $F$ 只含一棵树为止。

利用上述原理，我们可以介绍赫夫曼编码，我们设需要编码的字符集为 ${d_1,d_2,…d_n}$，各个字符在电文中出现的次数或频率集合为 ${w_1,w_2,…w_n}$, 以 $d_1,d_2,…d_n$ 作为叶结点，$w_1,w_2,…w_n$ 作为相应的叶结点的权值来构造一棵赫夫曼树。规定左分支代表0，右分支代表1，则从根结点到叶结点所经过的路径分支组成的0和1的序列便为该节点对应字符的编码，称为 赫夫曼编码。