抽象代数自学笔记3:环与域
环与域-更多内容
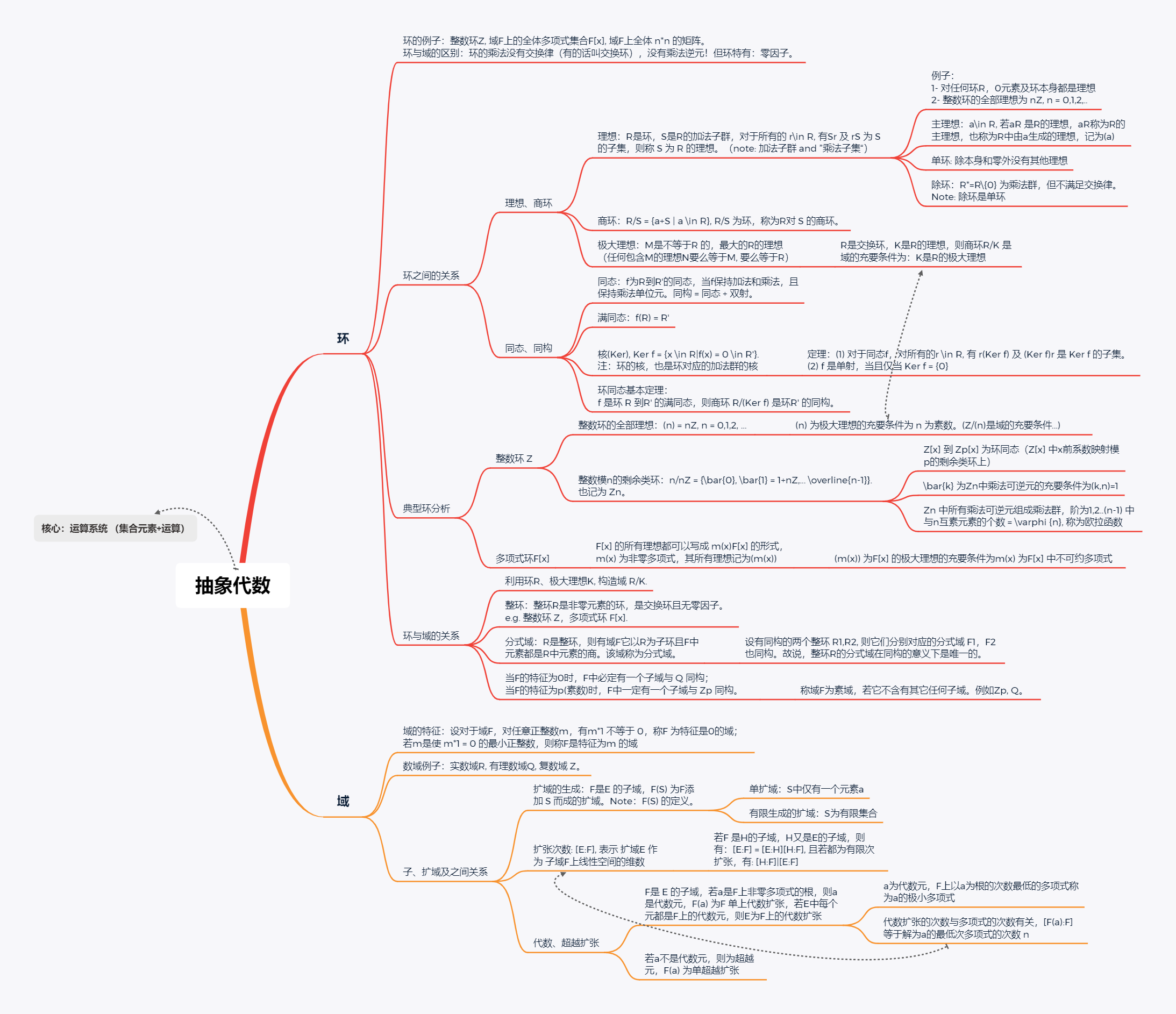
对于抽象代数来讲,由于群是最基础的结构,群部分的内容通常更加重要,环和域的很多内容都是在群的相关理论的基础上进行一些的更改、变形。
一些典型的环和域的例子有,环:整数环$Z$, 域$F$上的全体多项式集合 $F[x]$ 为环,域 $F$ 上的全体 $n*n$ 的矩阵为环。域:实数域$R$, 有理数域$Q$, 复数域$Z$.
I 环的同态与同构
由于相比于群多了加法运算,环的同态同构条件要强于群。如下:
定义1 同态and同构
设 $R$, $R’$ 是两个环,$\varphi$ 是 $R$ 到 $R’$ 的映射,如果:
$\varphi$ 保持加法,即 $\forall x,y\in R$, 有 $\varphi(x+y) = \varphi(x) + \varphi(y)$;
$\varphi$ 保持乘法,即 $\forall x,y \in R$, 有 $\varphi(xy) = \varphi(x)\varphi(y)$,
$\varphi(1_R) = 1_{R’}$.
则称 $\varphi$ 为环 $R$ 到环 $R’$ 的同态。若 $\varphi$ 还是双射,则称 $\varphi$ 为$R$ 到 $R’$ 的同构。称 $\varphi$ 是 域$F$ 到 域$F’$ 的同态(或同构),若它是 $F$ 和 $F’$ 作为环的同态(或同构)。
类似于群同态,对于环同态,我们也定义同态的象和核。
定义2 满同态and核
设 $\varphi$ 是环 $R$ 到 $R’$ 的同态,令:
$\varphi(R) = {\varphi(x)|x\in R}$
称为 $R$ 在 $\varphi$ 下的象,若 $\varphi(R) = R’$,则称为 满同态。令:
$Ker \varphi = {x\in R|\varphi(x) = 0\in R’}$,
称为 $R$ 在 $\varphi$ 下的核。
Note: 实际上,$Ker \varphi$ 是 $R$ 到 $R’$ 的环同态核,又$R$ 和 $R’$ 是加群,$\varphi$ 也是加群的同态,$Ker \varphi$ 也是加群同态的核。
定理:环同态基本定理
- $R,R’$ 是环,$\varphi$ 是 环$R$ 到 环$R’$ 的满同态。令 $K = Ker\varphi$, 则商环 $\frac{R}{K}$ 与环 $R’$ 同构。
Note: 类似群同态基本定理。
II 理想和商环
理想是环中类似于群中的正规子群的概念,但不同的是,环的理想会涉及到乘法、和加法两种运算。
定义1:理想
$R$ 是环,$S$ 是 $R$ 的加法子群,且 $\forall r\in R$ 有 $Sr\subseteq S$ 及 $rS\subseteq S$,则称 $S$ 为 $R$ 的一个理想。
定义2:商环
(接定义1)$\frac{R}{S} = {a + S|a\in R}$
$\frac{R}{S}$ 是一个环,称为 $R$ 对 $S$ 的商环。
例子
a. 任意环 $R$ 中,零元素构成的集合以及 $R$ 本身都是 $R$ 的理想;
b. 整数环 $Z$ 的全部理想为 $nZ, n = 0,1,2, …$ ;
c.若 $R$ 是交换环,$a\in R$,则 $aR$ 是 $R$ 的理想,称它为 $R$ 的 主理想,或说,是 $R$ 中由 $a$ 生成的理想,$aR$ 常记为 $(a)$。
d. 非交换环 $n\times n$ 的矩阵 $M_n(F)$ 的理想只有零元和其自身两个。
定义3: 极大理想环
设 $R$ 是环,$M$ 是 $R$ 的理想,但不等于 $R$, 对 $R$ 的任何包含 $M$ 的理想 $N$, 若 $N\neq M$, 则 $N = R$, 这是称 $M$ 为 $R$ 的极大理想。
定理
设 $R$ 是交换环,$K$ 是 $R$ 的理想, 则 $\frac{R}{K}$ 是域的充要条件是 $K$ 为 $R$ 的极大理想。
理解:通过极大理想,可以通过一个环构造出一个域。
III 典型环分析
a. 整数环
对于整数环 $Z$, 它的全部理想是 $(n) = nZ, n = 0,1,2,…$. 作商环:
$\frac{Z}{nZ} = { {\bar{0} = 0+nZ},\bar{1} = 1+nZ, … \overline{n-1} = (n-1) + nZ }$
它称为整数模n的剩余类的环。它是n个元素的交换环,也记为 $Z_n$.
整数环的理想
对于整数环的理想 $(n)$ 何时为极大理想, 有 定理:
$Z$ 的理想 $(n)$ 为极大理想的 充要条件 是 n 为素数。
进一步的,根据这一特性,可以利用该极大理想的商环得到一个域: $Z/(n)$.
整数模n的剩余类环
对于整数环的理想的商环:整数模n的剩余类环,有如下 定理:
设 $\bar{0} \neq \bar{k}\in Z_n$, 则 $\bar{k}$ 是 $Z_n$ 中乘法可逆元,当且仅当 $(k,n) = 1$. ($k,n$ 互素)
推论
$Z_n$ 中所有可逆元组成乘法群,它的阶是 $1,2, … ,n-1$ 中与 $n$ 互素的元素的数目,这一数目也称为 欧拉函数, 记为 $\varphi(n)$。
b. 多项式环
有 $F[x]$ 是域 $F$ 上的多项式环,$N$ 是 $F[x]$ 的非零理想,则有非零多项式 $m(x)$,使得 $N = m(x)F[x] =(m(x))$,即该理想是由非零多项式 $m(x)$ 生成的理想,也就是说,$F[x]$ 的每个理想都是主理想。
多项式环的极大理想
类似整环的极大理想,对于多项式环,有定理:
$F[x]$ 的理想 $(f(x))$ 是 $F[x]$ 的极大理想的充要条件是 $f(x)$ 为 $F[x]$ 中的不可约多项式。
Note: $F[x]$ 表示的是多项式;$F(x)$ 则表示的是多项式分式。
IV 环与域的关系
我们知道向整数环中添加元素的商,就可以得到有理数域,那么什么样的环有这样称为域的 “潜质”。我们有定义:
定义1:整环
设 $R$ 是非零元素的环,若它是交换环且无零因子,则称 $R$ 为 整环。整数环 $Z$, 域上多项式 $F[x]$ 都是整环。域也是整环。
整环可以拓展成域:定理1
设 $R$ 是整环,则有一个域 $F$, 它以 $R$ 为子环且 $F$ 中元素都是 $R$ 的元素的商。这个域 $F$ 称为 $R$ 的 分式域。
此外,整环还具有如下性质:定理2
设 整环$R_1$与$R_2$同构,他们分别有分式域 $F_1$ 与 $F_2$, 则$F_1$ 与 $F_2$ 是同构的域。也就是说整环 $R$ 的分式域在同构的意义下是唯一的。
V 域的扩张
域可以通过添加元素进行扩张,例如向实数域中添加 $i$ 得到了复数域。普遍的,我们定义 扩域:
定义1:扩域
令 $E$ 是域,$F\subset E$, 若 $F$ 在 $E$ 的运算下也成为域,则称 $F$ 为 $E$ 的 子域,而 $E$ 称为 $F$ 的 扩域。
进一步的,$E$ 是 $F$ 的扩域,$S\subset E$, 称域 $F(S)$ 为 $F$ 添加 $S$ 而成的 扩域。如果 $S$ 中仅有一个元素 $\alpha$, 我们称 $F(\alpha)$ 为单扩域。
Note:
$$F(S) = { \frac{f_1(a_1,a_2,…a_k)}{f_2(a_1,a_2,…a_k)}|\forall a_i\in S, f_i(x_1,x_2,…x_n)\in F(x_1,x_2,…x_k),f_2(a_1,a_2…a_k)\neq 0 }$$
域进行扩张后,我们用扩张次数来描述扩张的程度,有,
定义:扩张次数
设 $E$ 是 $F$ 的扩域,以 $[E:F]$ 表示 $E$ 作为 $F$ 上的线性空间的维数, 称为 $E$ 对 $F$ 的扩张次数。若 $[E:F] = \infty$, 则称为 无限次扩域,若 $[E:F] = n$, 则称为有限次(n次)扩域。
扩张次数有如下 定理:
设 $F\subset H\subset E$ 是域的扩张,则$[E:F] = [E:H][H:F]$.
(推论)若 $E,H,F$ 都是有限次扩张,则有: $[H:F] | [E:F]$
此外,我们还根据用于扩张的元素的特性,将扩张进行分类:
代数元与代数扩张: $F\subset E$ 为域扩张,$\alpha \in E$, 若$\alpha$ 是 $F$ 上某一非零多项式的根,则称 $\alpha$ 为 $F$ 上的 代数元。而 $F(\alpha)$ 称为 $F$ 上 单代数扩张。若 $E$ 中每个元都是 $F$ 上的代数元,则称 $E$ 是 $F$ 上 代数扩张。
超越元与超越扩张:若 $\alpha \in E$ 不是 $F$ 上代数元,则称为 $F$ 上 超越元,$F(\alpha)$ 称为 $F$ 上 单超越扩张。
例子:$\sqrt{2}$ 是 $Q$ (有理数域) 上代数元,$\pi, e$ 是 $Q$ 上超越元。
环与域思维导图