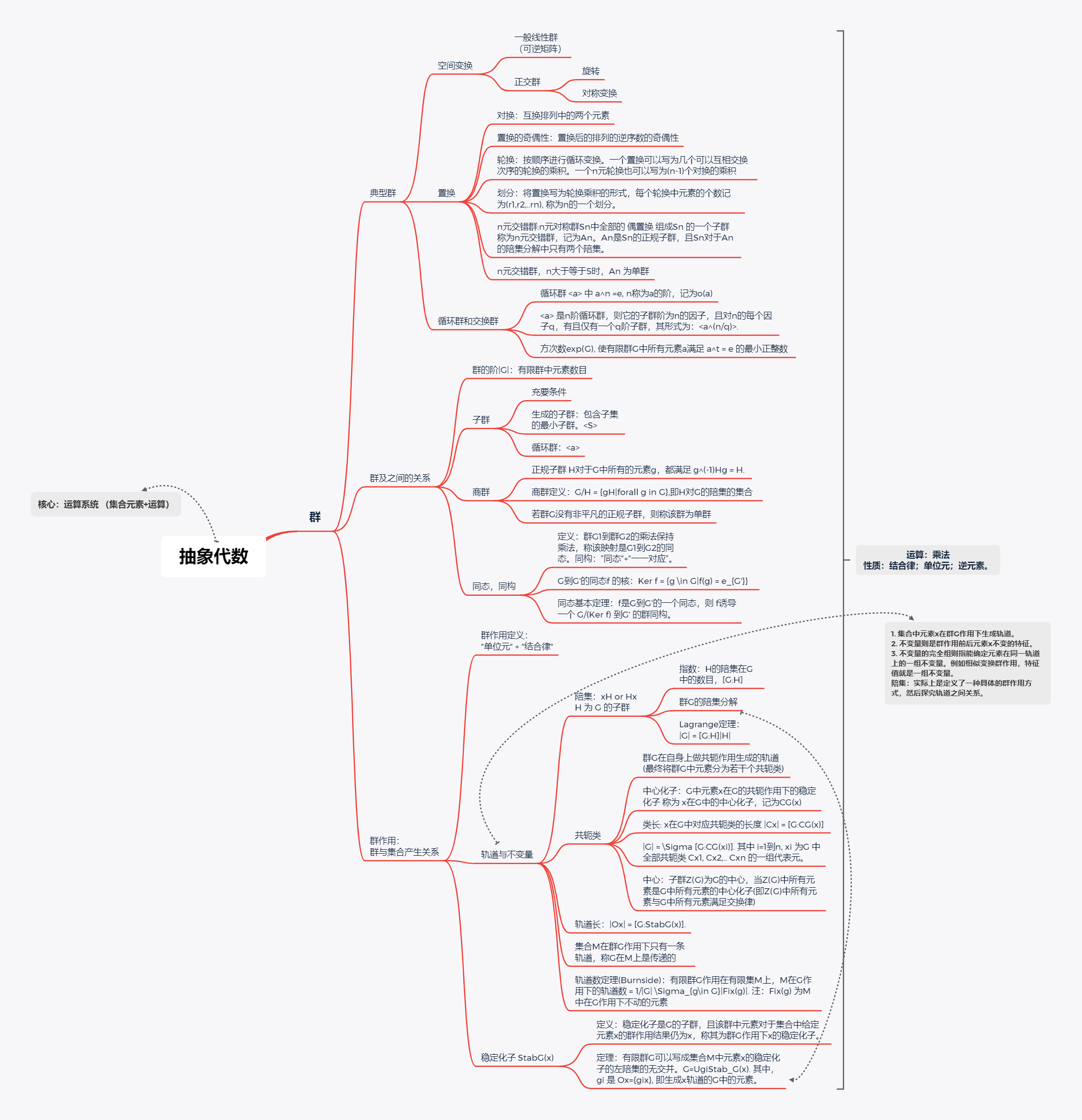
抽象代数自学笔记2:群
群的更多内容
群的所有基础相关知识,都以思维导图的形式进行了整理,所以文字部分,只将我认为重点的内容做进一步的强调和探讨。
I 群之间的关系-同态与同构
两个群 $G_1$ 及 $G_2$,若有 $G_1$ 到 $G_2$ 的映射 $\sigma$, 它保持乘法,即对 $\forall g_1, g_2 \in G_1$, 有 $\sigma(g_1g_2)=\sigma (g_1)\sigma (g_2)$, 则称 $\sigma$ 是 $G_1$ 到 $G_2$ 的同态,若 $\sigma$ 还是 $G_1$ 到 $G_2$ 的双射(or called 一 一对应),则称 $\sigma$ 是 $G_1$ 到 $G_2$ 的同构,通常用 $G_1 \cong G_2$ 表示 $G_1$ 与 $G_2$ 同构,群 G 到自身的同构称为 G 的自同构。
例子:
同态:
e.g.1: 整数加法群 Z,$n\in Z$, 与 nZ, 为 $nZ={kn | k\in Z}$, 也即 $nZ=\langle n \rangle$,构成群同态。映射 $k\rightarrow kn$ 为 Z 到 nZ 的同态。
e.g.2 n 阶可逆矩阵,通过行列式运算映射,与 $F$\|0| 同态。也就是 |AB| = |A||B|. 即行列式运算是 n阶可逆矩阵 到 F\|0| 的同态。
同构
e.g.1 V 是域 F 上的 n 维线性空间,V 上全体可逆线性变换的群 $GL(V)$ 与域 F 上全体 n*n 可逆矩阵的群 $GL_n(F)$ 是同构的。
e.g.2 $R^+$ (正实数)上的乘法群,与 $R$ 实数上的加法群,通过取对数一一对应,i.e. $R^+ (通过log)\rightarrow R$, 因为任意一正实数 a 可以表示成 $10^{a^\prime}$ 的形式。 我们称取对数 log 这个映射是 $R^+$ 到 $R$ 的同构映射。(因此,计算中可以将乘法通过取对数转化为加法,计算完成后再转回,来简化计算)
定理:同态基本定理
设 $G,\bar{G}$ 是两个群及 $\pi$ 是群同态 $G\rightarrow \bar{G}$, 且是满同态,令:
$K = {g\in G| \pi(g) = e_{\bar{G}}} = Ker\ \pi$
是同态 $\pi$ 的核,则 $K$ 是 $G$ 的正规子群,且$\pi$ 诱导一个从商群 $\frac{G}{K}$ 到 $\bar{G}$ (即$\pi(G)$) 的群同构。
理解:群同态基本定理提供了一种由同态关系推导出同构关系的方法。
II 群作用, 集合在群作用下的不变量及群的划分
定义1:轨道
群$G$ 作用于 集合 $M$ 上,对 $x\in M$,称集合:
$O_x = {g\circ x | g\in G}$
为 元素$x$ 在 $G$ 作用下的轨道,或简称过 $x$ 的轨道。
理解:
(1)例如 绕 $x$ 轴 的 旋转作用群 $G$,对于平面空间点集中的一点 $x$ 作用, 得到一个以 $x$轴 为中心的圆,该圆称为 点$x$ 在 $G$ 作用下的轨道。
(2)在“同一条轨道上”,实际上是$M$上的一种等价关系,类似矩阵中的合同及矩阵的相似。
定义2:稳定化子
设群 $G$ 作用于 $M$。对 $x\in M$, 令:
$Stab_G(x)={g\in G|g\circ x = x}$. 称它为群 $G$ 作用下 $x$ 的稳定化子。
理解:稳定化子是 $G$ 的子群,可以理解为让集合中元素 $x$ 稳定的那一部分群元素(对应的群作用)。
定义3:陪集
考虑有限群 $G$, 令 $G$ 的子群 $H$ 在 $G$ 上作左乘作用,对 $x\in G$, 这个群作用下过 $x$ 的轨道: $Hx = {h\circ x = hx|h\in H}$,称为 $H$ 在 $G$ 中的一个右陪集,
而 子群 $H$ 在 $G$ 上右乘作用下过 $x$ 的轨道,$xH = {x\circ h^{-1} = xh|h\in H}$, 称为 $H$ 在 $G$ 中的左陪集。
定义4:指数,陪集分解
子群 $H$ 在 $G$ 中左(右)陪集的数目称为子群$H$ 在 $G$ 中的 指数,记为: $[G:H]$.
下面等式第一(二) 个等号后面的式子称为子群$H$ 对于 $G$ 的右(左) 陪集分解。$G = \cup^s_{i=1} Hg_i = \cup^t_{j=1} g_j’H$.
理解:也就是说 群 $G$, 可以依据自己的一个子群 $H$ 进行划分,划分为 $H$ 的一个个陪集。
定理1:Lagrange 定理
$G$ 是有限群,$H$ 是 $G$ 的子群,则:
$|G| = [G:H]|H|$.
定理2:根据稳定化子划分群
$G$ 是有限群, $G$ 在 $M$ 上有群作用,对 $x\in M$, 令 $O_x$ 是过 $x$ 的轨道,$O_x= {g\circ x|g\in G}$ 是有限集。 设 $O_x = { x_1,x_2,… x_k}$,其中 $x_1 = x$. 且设 $g_1,g_2, …g_k\in G$ 使 $x_i = g_i\circ x, i = 1,2, … k,$ 则:
$G = \cup^k_{i=1}g_i Stab_G(x)$, 即 $G$ 可以写成 $Stab_G(x)$ 对 $G$ 的左陪集的无交并。
理解:上面 定义4 说到 群$G$ 可以根据它的一个子群进行划分,这里,这个子群为一个特殊的子群,为集合 $M$ 中元素的稳定化子 $Stab_G(x)$。在这样的条件下,我们还可以更进一步的找到所有的 用于生成陪集的元素 $g_i$。
推论1:轨道长
轨道长 $|O_x|$ 满足公式 $|G| = |Stab_G(x)||O_x|$ 或 $|O_x|=[G:Stab_G(x)]$
III 群依据共轭类的划分
定义1:共轭类
群 G 在自身上作共轭作用的轨道叫做 G 的一个共轭类。
补充: G是一个群,他在自己身上的3个作用:左作用:$L_h(g)=hg$; 右作用:$R_g(g)=gh^{-1}$, 共轭作用: $\sigma_h(g) = hgh^{-1}$.
定义2:中心化子
$G$ 的元素 $x$ 在 $G$ 的共轭作用下的稳定化子称为 $x$ 在 $G$ 中的中心化子, 记为 $C_G(x)$, $C_G(x) = {g\in G|gxg^{-1}=x} = {g\in G | xg=gx}$
理解:类似稳定化子。
定理:类长与类方程
$G$ 中含 $x$ 的共轭类中的元素数目即类长 $|C_x|$, 等于 $[G:C_G(x)]$. 设 $C_{x1}, C_{x2} …C_{x_n}$ 是 G 的全部共轭类,即$(x_1, … x_n)$ 是 $G$ 的全体共轭类的一组代表元,则:
$|G| = \Sigma^n_{i=1}[G:C_G(x_i)]$.
理解:实际上与使用稳定化子划分群非常类似。
IV 商群
定义2:正规子群
$G$ 是群,$H$ 是 $G$ 的子群。若 $\forall g \in G$,有 $g^{-1}Hg = H$, 则称 $H$ 为 $G$ 的 正规子群, 记为 $H\triangleleft G$.
命题2:商群
设 $G$ 是群,$H\triangleleft G$, 记 $H$ 对 $G$ 的陪集的集合为:
$\frac{G}{H} = {gH | g\in G}$
则 $\frac{G}{H}$ 对于陪集的乘积成为一个群,称为 $G$ 对 $H$ 的商群。
Note:当在上下文中 $H$ 是给定的,我们常常可以略去 $H$ 进行表示。具体的,将 $\frac{G}{H}$ 写为 $\bar{G}$, 元素 $gH$ 写为 $\bar{g}$。
例子:对于整数加法群 $Z$,它的任一正规子群为 $\langle n\rangle$, 也即 $nZ$, 加群的陪集形为 $k + nZ$, $Z$ 的对于子群 $nZ$ 的商群为:$\frac{Z}{nZ} = {nZ,1+nZ, … (n-1+nZ)}$. $Z$ 对 $nZ$ 的 陪集 也常称为模 $n$ 的 同余类 或 剩余类。
从上述例子可以看出,通过商群的概念,得到了一个比原先群简化的群,它继承了原来群的乘法概念,但更简单,更利于分析。
群-思维导图